回帰分析とは?
今回は統計学の基本要素である回帰分析についてみていきます。私もそうだったのですが、データ分析を勉強し始めた人が皆ぶつかる壁が、「分析ってなんやねん」という疑問です。
漫画とかでは、テニプリの乾みたいなキャラが分析分析と簡単に言いますが、リアルでデータを集めてこれをいざ分析となると何をしたらいいんだってなります。同じように、最近テレビとかでもビッグデータや分析力という言葉が頻繁に使われるようになりましたが、データサイエンスの観点でデータを見る目的は、「獲得したデータを分析し、いかに将来を予測するか」です。
獲得するデータには、マーケティング目的であれば、アンケートデータ・購買データ・WEBの閲覧データetc…株価予測であれば財務情報・株価データなどがあります。
まあどのようなデータにしても、「そのデータを分析することでデータの特徴をよく知り、将来の動きを予測することによって、有用な知見を得ること」が目的なのです。
データの特徴を知る方法というのはこれまで紹介してきた平均・分散といった基本統計量やグラフ化というのがあります。
⇨【統計学】平均・中央値・最頻値について ~基本統計量 その1
そして、データの予測の具体的な方法というのが、今回のテーマである回帰分析となります。この回帰分析はデータ分析による予測の超基本であり、大きく「単回帰分析」と「重回帰分析」に分類されます。
今回は1つの変数でもう1つの変数の動きを予測する、「単回帰分析」について説明していきます。(具体例でいうと、身長から体重を予測するなど)
単回帰分析とは?
単回帰分析というのは、2つ変数の関係性をY=aX+bという一次方程式の形で表す分析です。つまり、a(傾き)とb(Y切片)がわかれば、XからYの数値を予測することができるわけで、このaとbを求める分析といえます。(ちなみにこのaとbは回帰係数といいます。)
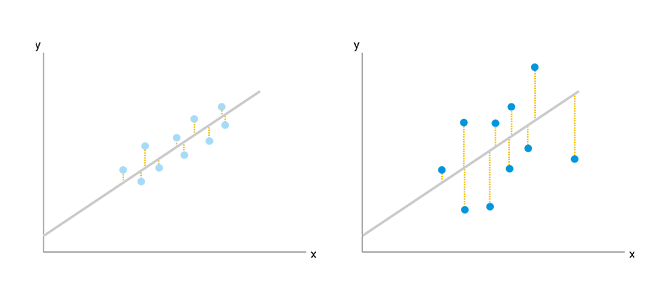
そして、このaとbはどのようにして求めるのかというと、「最小二乗法」という誤差の二乗の和を最小にする方法を用います。この方法は「単回帰分析」だけではなく、「重回帰分析」においても用いられます。
最小二乗法による回帰係数の求め方
「最小二乗法」による回帰係数の計算はエクセルでやれば、向こうが勝手に計算してくれるのですが、一応でのような計算が行われているのか見ていきます。

(参照:http://xica.net/8v6t1phd/)
それぞれの変数の平均値を求める
↓
それぞれの変数の偏差(数値 - 平均値)を求める↓
変数 x の分散(偏差の二乗平均)を求める↓
共分散(偏差の積の平均)を求める↓
共分散を変数 x の分散で割って回帰直線の傾きを得る↓
2 つの変数の平均値と傾きから、回帰直線の y 切片を得る
ちなみにエクセルでは回帰分析を行うと、傾き (slope)と切片( intercept )に加えて決定係数R²(rsq )と相関係数 (correl) も計算してくれます。
相関係数と決定係数
相関係数と決定係数はが、どれくらい信憑性があるのかをあらわす数値です。ちなみに相関係数については下の記事で解説しています。
まあ要するに、2つの変数の数値の変化にどれくらい相関があるのかを、-1~1の範囲であらわしたもので、相関係数の絶対値が大きいほど相関関係があるということになります。
そして、決定係数というのは、決定係数とは回帰モデル(計算によって求められたaとbの値)によって変数(データ)をどれくらい説明できているか、つまり回帰分析の精度を表す指標です。
決定係数は基本的に0から1の範囲で表され、 1 に近いほど 残差変動が小さい、つまりよい回帰モデルであるとみなすことができます。ちなみに計算上はひどいモデルであれば決定係数をマイナスになりえます。
決定係数は一般的に R²で表され、相関係数の2乗の値となります。基本的に回帰分析をした際にモデルの決定係数R²が0.5以上あれば、そのモデルは有効であるといえます。
追記:統計学の初歩的学習にはコチラの「マンガでわかる統計学入門」という本が分かりやすかったので紹介しておきます。


コメント