こんにちは、ミナピピン(@python_mllover)です。今回はデータ分析の業務でよく行う「クラスタリング」の手法の1つである「主成分分析(PCA)」について解説していきます。
主成分分析(PCA)とは
機械学習はデータと正解との関係性をモデルに学習させて正解を予測します。
- データ:特徴量や説明変数と呼ばれる。正解を説明するデータ群
- 正解:目的変数やラベルと呼ばれる。予測対象
ここで説明変数の中に、お互いに相関関係にある複数の説明変数が存在すると、モデルはそれらの説明変数の影響を強く受けてバイアスがかかった状態となってしまいます。その状態を解消するのが主成分分析(PCA)です。
主成分分析は「相関関係にある複数の説明変数」を相関関係の少ない説明変数にまとめます。これにより説明変数の相関によるバイアスが軽減され、モデルはより適切な学習を行えるようになります。これは実務でも良く使う手法で、これによる説明変数の項目を減らす(次元圧縮)を目的として行うことが多いです。
テストデータを用意する
今回はサンプルデータとしてscikit-learnに付属しているおなじみのアヤメの花弁のデータを使用します。
# データセットを読み込み from sklearn.datasets import load_iris iris = load_iris() # Pandas のデータフレームとして表示 import pandas as pd df = pd.DataFrame(iris.data, columns=iris.feature_names) # データの確認 df.head()
各説明変数を標準化する
まず(第1列目以外の)各列に対して、平均値を引いたものを標準偏差で割り、各説明変数の数値を標準化します。
# 各説明変数を標準化する dfs = df.iloc[:, 1:].apply(lambda x: (x-x.mean())/x.std(), axis=0) dfs.head()
ちなみに主成分分析(PCA)で合成変数を作成する場合、2つのパターンがあります。
① 各変数のレベル(位置)をそろえる(平均を同じにする,平均からの偏差にする)。
②各変数の得点のレベル(位置)とばらつきの大きさの双方をそろえる(平均と標準偏差を同じにする,基準化(標準化)する)。
単位が異なる複数の変数を扱う場合は,②の基準化を行って単位をそろえる必要があります。単位が同じ場合は①と②の双方の立場で分析が可能です。①では各変数の分散の大きさを考慮した係数が求まり②では各変数の分散の違いを無視した係数が求まります。①②のどちらを採用すべきかという議論については、以下でまとめてくださっている情報が詳しいです。
⇒https://qiita.com/koshian2/items/2e69cb4981ae8fbd3bda
要は主成分分析で標準化(標準偏差で割る)するのが必ずしもいいとは限らないし、それどころか標準偏差で割ることは悪影響もあるので標準化すべきかどうかは、どこで主成分分析を使うか(可視化として使うのか、パイプラインとして使うのか)によっても異なるからそこをちゃんと考えましょう
なので標準化に関しては必ずしも行う必要はないですし行う意味を考えましょうて感じですね。これで前準備は完了です。次から主成分分析を行っていきます。
Pythonで主成分分析を実装する
いよいよ本題の主成分分析を実装していきます。
# データを主成分分析にかける from sklearn.decomposition import PCA pca = PCA(n_components=2) pca.fit(dfs)
n_componentsは主成分を幾つ求めるかを指定しています。’mle’ を指定すると最尤推定により個数を⾃動的に求め、 0〜1の間の実数を指定すると累積寄与率がその値になるまで主成分を求めます。これによって3つの説明変数を意味を持たせたまま2つに圧縮することができました。これを一般的に「次元圧縮」と言います。この次元圧縮のためにPCAを使うことが実務だと結構あります。
これで分析は完了です。ライブラリを使えば分析自体は一発で完了します。次は分析結果の解釈に入っていきます。まあこっちが本命ですね。主成分分析の場合は寄与率と因子負荷量をまず確認します。
# 寄与率と因子負荷量をまず確認 import numpy as np print(pca.explained_variance_ratio_) print(np.cumsum(pca.explained_variance_ratio_)) print(pca.components_ * np.sqrt(pca.explained_variance_)[:, np.newaxis])
<実行結果>
寄与率⇒[0.74049445 0.24793475] 累積寄与率⇒[0.74049445 0.98793475] 因子負荷量⇒[[ 0.62318947 -0.96621871 -0.94844063] [ 0.78200405 0.22037075 0.28932791]]
寄与率
• 端的に⾔えば各変数がどれくらいの重要なのかという重要性を表しています
• 各主成分によって説明できるデータの割合を表す
→ 全ての主成分の寄与率を⾜し合わせると1.0になる
因⼦負荷量
• 各変数の各主成分への影響⼒ → 各主成分の意味を推定できる
累積寄与率が0.98なので、主成分2つでsepal length (cm)の98%が説明できることになります。また因子負荷量を見るとsepal width (cm)の数字が大きいので、これがsepal length (cm)の大きさの大きな因子であることが伺えます。
データのプロット
# データを主成分空間に写像 feature = pca.transform(dfs)
# 主成分得点
test_data = pd.DataFrame(feature, columns=["PC{}".format(x + 1) for x in range(2)])
test_data
range(2)なのは3つの説明変数をPCAで2つに次元圧縮したからです。
# 第一主成分と第二主成分でプロットする
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(6, 6))
plt.scatter(feature[:, 0], feature[:, 1], alpha=0.8, c=list(df.iloc[:, 0]))
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()
plt.scatterの引数のdf.iloc[:, 0]は今回の正解ラベルにあたるdf[‘sepal length (cm)’]です。これによってグラフ上の点を対応するsepal length (cm)の長さによって色付けしてくれます。
<実行結果>
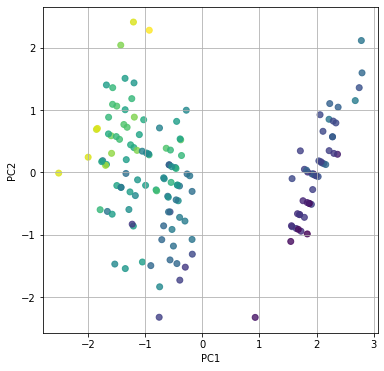
なんとなく特徴量での分類ができています。主成分分析による次元圧縮を行い、その特徴量によるクラスタリングは機械学習などで使用するデータの質をそろえるためによく使われるテクニックなので覚えておきましょう(自分へのブーメラン)
関連記事:【Python】pandas-datareaderでVIX(恐怖指数)を取得してk-Mean法でクラスタリング




コメント
[…] 参考記事:【Python】主成分分析(PCA)で学習データをクラスタリングする […]
[…] 参照:【Python】主成分分析(PCA)でのクラスタリングを実装する […]