統計検定の教科書が改訂されたみたいなので読んでみました。多少はマシになったものの相変わらずの意味不明さはあったので、特に4章の統計的仮説検定の部分のパターンを整理しておきます。
統計的仮設検定の種類を把握する

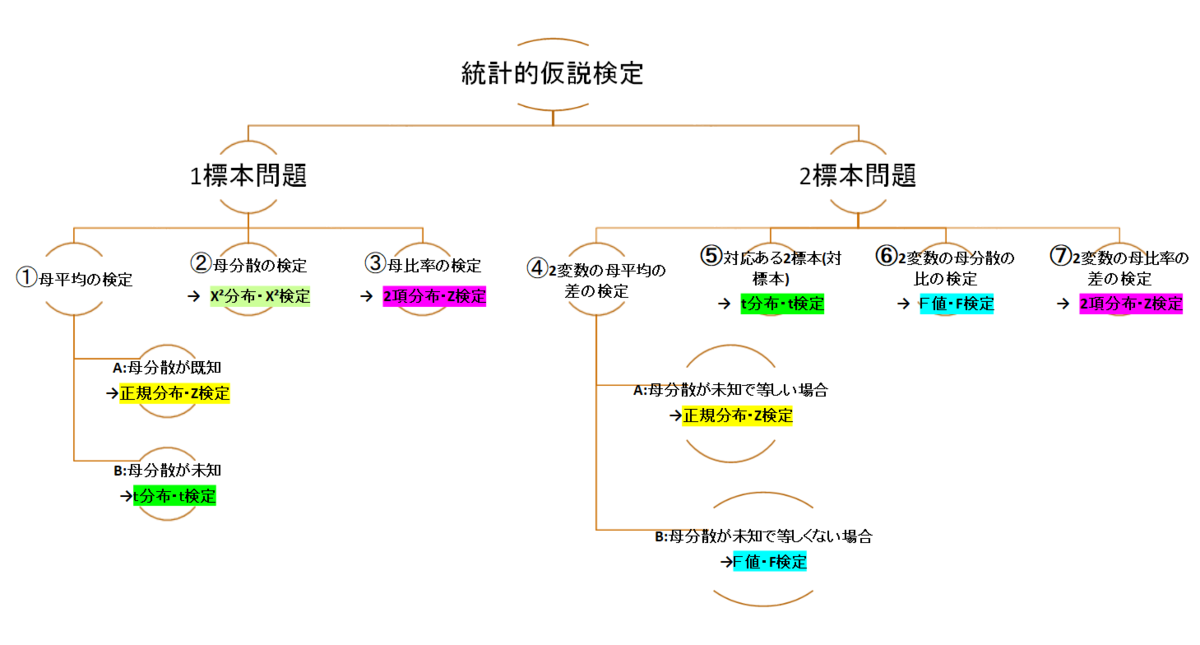
統計検定2級の問題範囲にある統計的仮設検定の問題パターンは大きく分けて7種類、9パターンあります。加えてここに場合によって、両側検定になるものと片側検定になるものが存在しているという感じです。
統計検定2級に受かるためには、片側か両側かの検定自体のパターン把握とこの9パターンの解き方を覚える必要があります。
コイントスで帰無仮説と対立仮説の設定方法とp値の意味を超分かりやすく説明する
片側検定と両側検定の違いと問題での判別方法
検定の覚え方
平均云々→ 正規分布 → z検定 or t検定 (2標本かつ等しくないときはF検定)
分散云々→ 変な分布 → Χ²検定・F検定
比率云々→ 2項分布(標本数多いから実質正規分布) → z検定(2項分布版)※
※標本数が少ない場合は2項分布の公式で解くときもある
z→標準正規分布のx軸の数値
t,Χ²,F→各分布のx軸の数値
基本的にz検定とt検定は分散σに標本分散を使うか、母分散を使うかの違いなので、覚えやすい。Z検定(2項分布版)も式が簡単なので覚えやすい。めんどくさいにはΧ²分布とF分布、こいつらを頑張って覚える
問題パターン一覧
①1標本問題における母平均の検定
②1標本問題における母分散の推定
③1標本問題における母比率の推定
④2標本問題における母平均の差の推定
⑤2標本問題における対標本の推定
⑥2標本問題における母分散の比の検定
⑦2標本問題における母比率の差の検定
統計的仮説検定の問題の解き方
①検定の種類(1標本or2標本、平均・分散・比率、母分散があるかどうか)と検定方法(片側or両側)を判別する
②それぞれの検定の検定統計量(z値,t値 ,Χ²値,F値)を計算する
③設定してある有意水準からα値を計算する(両側検定ならα→α、片側検定ならα→α/2)。例えば有意水準5%の両側検定ならα=0.05、片側検定ならα=0.05÷2=0.025となる※2
⑤z検定などはわざわざαを出さずとも先にP値に対応する検定統計量と照らし合わせることでも行える。またt検定などでは計算した検定量(t値)からでは、PCがないと正確なαを出すことが難しいためα=0.05,0.025に対応した検定量(t)との大小を比較して帰無仮説を棄却できるかを判断することが一般的です。
参考資料


コメント