大数の法則によって、標本平均は母平均 µ のまわりに分布し、µ から離れる確率は n が大きくなるにつれて 0 になります。
このとき、標本平均 X の平均と分散の値だけでなく、標本平均X の分布も中心極限定理はよって求めることが可能です。
ちなみに、この定理は母集団の平均と標本平均についてのものなので、「母分布が正規分布とは異なる一様分布であっても、n が十分に大きければ標本平均 X の分布は正規分布 N(µ,σ2/n) によって近似できる」ということも意味しています。
中心極限定理を利用するための条件は、母分布の平均と分散が存在することなので、母集団の分布の形はわかっていなくても大丈夫です。
つまり、中心極限定理により標本分布がわからない場合や、分布が複雑すぎて確率密度の計算が困難な場合でも、n が十分大きければ、中心極限定理により正規分布を仮定して、推定や検定を行うことが可能なのです。
ちなみに中心極限定理が適用できる n の大きさは 30 ∼ 100 以上とされることが多いです。

例題 :ある工場で作られるネジの重さは過去の記録から平均 100グラム,標準偏差 σ が 5グラムであったとする。ある日この生産工程より 100コのネジを抜き出し、重さの品質調査を行うことになった。
(1) 100コのネジの平均重量が100グラム以上で 105グラム以下である確率を求めよ。
(2) 標本平均が 95 %の確率 を伴って入る区間 (a,b) を求めよ。
解答(1)
要するにP(100 ≦ X≦ 105) を求めるという事になります。
中心極限定理によりnが大きければ ( n ≧ 100)、母分布がいかなる分布でも、母平均 µ と母分散 σ² が既知であれば、 X を標準化した Z を標準正規分布で近似できます。
すなわち、
E(X) = µ = 100, σ/√n = 5/√100 = 1/2 = 0.5
Z = X −100 /0.5
.
P(100 ≦ X≦ 105) = P(100−100/ 2.5≦ Z ≦105−100 /2.5 )
= P(0 ≦ Z ≦ 2) =0.4772(標準正規分布表より)
→ 100コのネジの平均重量が 100グラム以上で 105 グラム以下の確率は 47.72%
解答(2)
この問題はつまりP(a ≦ X≦ b) ≈ 0.95 であるような a、b を求めろという事なので、まず標準正規分布表より、P(−c ≦ Z ≦ c) ≈ 0.95 であるような c を求めます。
標準正規分布は左右対称なので、 P(Z ≧ c) = (1−0.95)/2 = 0.025、P(Z ≦ c) = 1−P(Z ≧ c) = 1−0.025 = 0.975。標準正規分布表で 0.975 を探すと、c = 1.96 と求まり、P(−1.96 ≦ Z ≦ 1.96) ≈ 0.95 が得られる。
P(a ≦ X≦ b) ≈ 0.95 P(a−100/2.5 ≦ Z ≦ (b−100/2.5 )≈ 0.95
a−100/2.5 = −1.96 を変形して→ a = 2.5 × (−1.96) + 100 =95.1
b−100/2.5 = 1.96 → b = 2.5 × 1.96 + 100 = 104.9
よって P(95.1 ≦ X≦ 104.9) ≈ 0.95、つまり、母平均が 100 グラムであれば、標本平均が 100 時間から±4.9 時間 (= 2.5 × 1.96) から外の数値になるのは 100 回のうち 5 回程度だという事になります。
統計学についてしっかり勉強するのであれば、↓の本が分かりやすく説明していてオススメです。



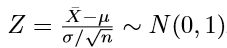
コメント