こんにちは、ミナピピン(@python_mllover)です。今回はPythonでの重回帰分析の手順についてメモ的にまとめておこうと思います。
使用するデータ
というわけでまず「statsmodels」で重回帰分析を実装してみましょう。使用するデータはscilkit-learnにあるボストンの住宅価格データです。こちらもタイタニックアヤメレベルで有名ないつものやつです。
import pandas as pd import numpy as np import statsmodels.api as sm from sklearn.datasets import load_boston boston_dataset = load_boston() # 説明変数をデータフレームにして先頭だけを可視化 boston_data = pd.DataFrame(boston_dataset.data, columns=boston_dataset.feature_names) boston_data.head()
変数boston_dataの中身はボストンの住宅価格に関連する説明変数で以下のようになっています。

参照:https://ai-kenkyujo.com/2020/08/24/ai_regression-analysis/
今回の分析は住宅価格の予測で、目的変数の住宅価格のデータは以下で抽出できます。
target = boston_dataset.target
これでデータは用意できたので分析に移ります。
Pythonで重回帰分析を実装
分析のコードは以下です。
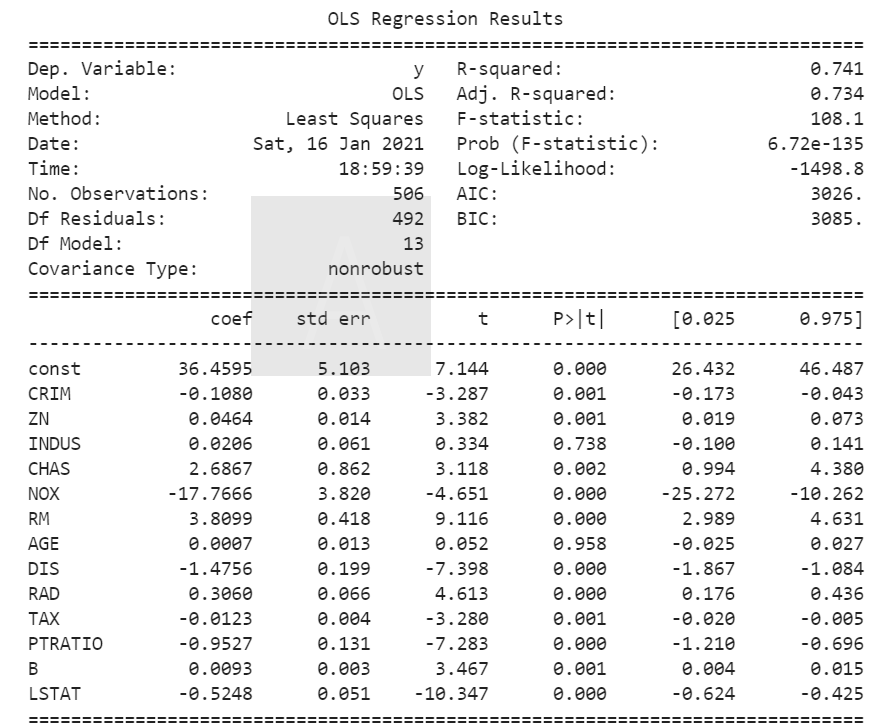
# 説明変数 X = boston_data # 目的変数 Y = target #回帰モデルの呼び出し model = sm.OLS(Y, sm.add_constant(X)) # モデルの作成 results = model.fit() #結果の詳細を表示 print(results.summary())
結果の解釈
R-squared:
決定係数。(1に近いほど精度の高いモデルであることを示す値)
Adj. R-squared:
自由度調整済み決定係数。決定係数は説明変数が増えるほど1に近づく性質があるため、説明変数が多い場合は、決定係数ではなく自由度調整済み決定係数の値を利用。
AIC:
モデルの当てはまり度を示す。小さいほど精度が高い。相対的な値である。
coef:
各変数の偏回帰係数、constは切片、pandasのデータだと変数ラベルがそのまま継承されるので見やすい、NUMPY行列だとX1、X2・・・みたいに表示される
std err :
二乗誤差
t:
t値。それぞれの説明変数が目的変数に与える影響の大きさを表します。つまり絶対値が大きいほど影響が強いことを意味します。1つの目安としてt値の絶対値が2より小さい場合は統計的にはその説明変数は目的変数に影響しないと判断します。
p:
p値。それぞれの説明変数の係数の有意確率を表します。一般的に、有意確率が有意水準以下(5%を下回っている)ならば、その説明変数は目的変数に対して「関係性がある=有意性が高い」ということを示す。
[0.025 0.975] 95%信頼区間。
参照:https://algorithm.joho.info/programming/python/statsmodels-olm/
#重回帰分析の統計量を見やすく出力する,
print('重決定R2:',results.rsquared),
print('補正R2:',results.rsquared_adj),
print('有意F:',results.f_pvalue),
print('切片',results.params[0]),
print('偏回帰係数'),
print('-------')
# const=切片,
print(results.params[1:]),
print('-------')
print('p値'),
print(results.pvalues),
print('-------')
print('t値'),
print(results.tvalues)
綺麗に整形されたデータなので、決定木係数は0.7とそこそこの精度がでていますね。
モデルから予測値を算出する
分析結果の切片と偏回帰係数からモデル予測値を計算し、実績値と比較してみましょう。
良い子の皆はデータフレームをfor文で回さないようにしましょう。
%matplotlib inline
data_pred = []
pred = 0
index = 0
for i in range(len(Y)):
for s in X.columns:
index += 1
pred += X[s].iloc[i]*results.params[index]
pred += results.params[0]
data_pred.append([Y[i], pred])
pred = 0
index = 0
pd.DataFrame(data_pred,columns=['y','y_pred']).iloc[:100].plot()
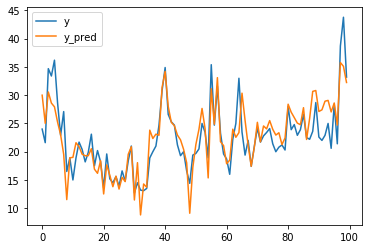
似たような動きになっているのが分かりますが、やはりスパイクしている部分がとらえきれていないかなというのが感想ですね。株価の予測とかはこのスパイクの部分の読み外しで死にます。


コメント