こんにちは、ミナピピン(@python_mllover)です。今日はPythonで時系列モデルの一種であるARMAモデルを実装して時系列データ予測をしてみたいと思います。
ARMAモデルの特徴
ARMAモデルはARモデルとMAモデルを組み合わせた時系列モデルです。
ARMAモデルは定常過程でしか使用できないので、モデルに当てはめる前にデータが定常過程であるかをADF検定で確認する必要があります。
⇒ 【Python】「ADF検定」で時系列データの定常性・単位根を確認する
使用するデータ
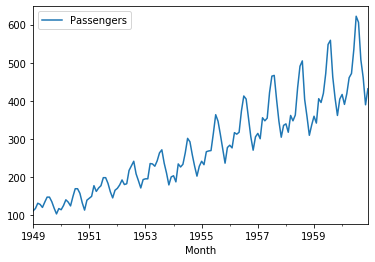
お馴染みの航空データのあれです。アイスクリームの売上データと同じで周期性が明確なのでサンプルにはうってつけです。
# ライブラリをインストールする $ pip install pydse
# ライブラリの読み込み import numpy as np from pydse import data import matplotlib.pyplot as plt %matplotlib inline df = data.airline_passengers() df.plot()
ARモデルでの時系列分析をPythonで実装する
# 変化率を計算する df['change'] = df['Passengers'].pct_change() # データを訓練用検証用に分割する train = df['change']['1949-02-01':'1953-12-01'] test = df['change']['1954-01-01':'1958-12-01'] # ライブラリの読み込み import statsmodels.api as sm from statsmodels.tsa.arima_model import ARMA # 次数の推定 print(sm.tsa.arma_order_select_ic(train, max_ar=5, max_ma=5, ic='aic'))
<実行結果>
{'aic': 0 1 2 3 4 5
0 -97.908137 -97.099831 -104.364375 -106.487216 -107.828935 -109.301734
1 -96.675481 -102.397764 -107.145821 -105.373528 -105.983293 -112.545341
2 -97.365209 -109.385341 -111.339383 -105.242073 -111.356696 -109.455262
3 -96.723783 -108.137864 -105.234977 -103.624707 -109.501827 -107.562090
4 -100.164411 -107.557020 -101.939387 -108.880098 NaN -105.104683
5 -98.183705 -105.750889 -103.207516 -101.818545 NaN -64.065413, 'aic_min_order': (1, 5)}
時系列モデルのラグの次数はAIC(赤池情報量規準)を見て選択します。AICが最小になるモデルが最適なモデルという事になります。基準尺度にはAICの他にもBIC(ベイズ情報量規準)というものも存在しています。実行結果に’aic_min_order’: (1, 5)とあるのでAIC基準で最適な次数は(1, 5)であることがわかります。
# テストデータでARMAモデルの作成と推定 arma_model = ARMA(test, (1, 1, 5)) result = arma_model.fit()
関数の引数は(p, d, q)なので(1, 1, 5)としています。真ん中のdは差分を意味していて今回は既に変化率で一次差分を取っているので1としています。
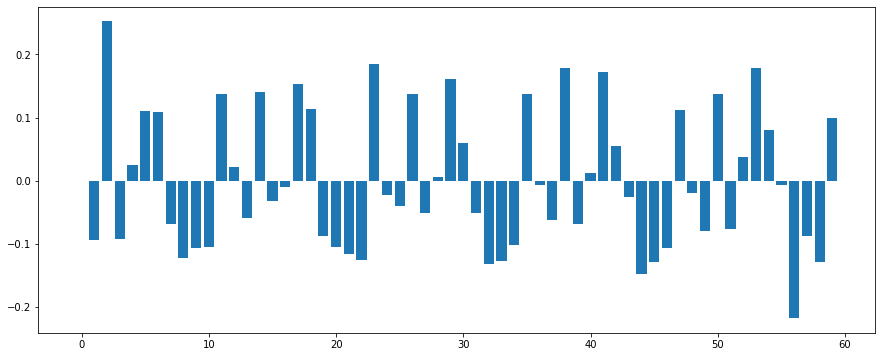
次にモデルの当てはまりの良さを確認するために残差を算出してプロットします。
# 結果の表示 print(result.summary()) # 残差を取得する arma_res = result.resid #残差プロット plt.bar(range(len(arma_res)), arma_res)
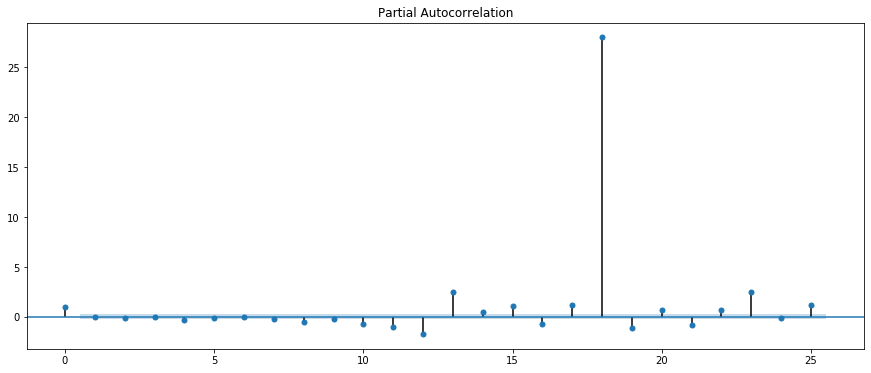
続いて残差の偏自己相関係数も確認してみましょう。
from statsmodels.graphics import tsaplots tsaplots.plot_pacf(arma_res, lags=40)
ほとんどが95%の有意水準からはみ出ている=統計的に有意な差があるので、この時点でモデルの当てはまりがあまりよくないことがわかります。
ARMAモデルで時系列予測
一応作成したARMAモデルを当てはめて訓練データを予測し比較してみます。
#予測
arma_model = ARMA(test, (1, 1, 5))
result = arma_model.fit()
arma_predict = result.predict('1954-01-01', '1958-12-01')
# 予測結果をプロット
plt.plot(test, label='observation')
plt.plot(arma_predict, '--', label='forcast')
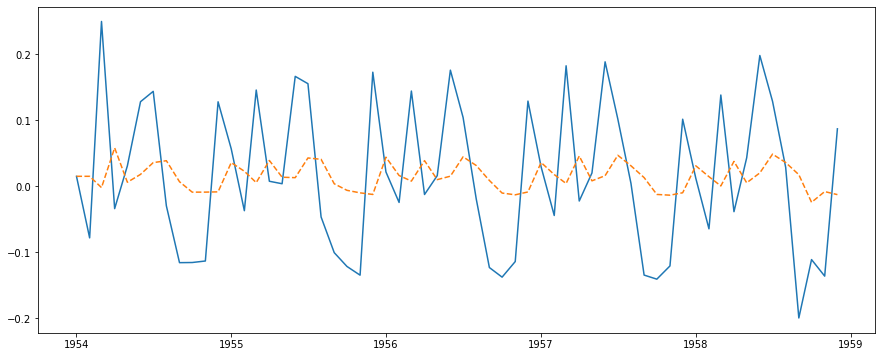
全然予測できてないですね・・・
⇒ 【Python】MAモデルによる時系列予測をやってみる
⇒ 【Python】VARモデルによる時系列予測をやってみる
⇒ 【Python】ARIMAモデルによる時系列予測をやってみる
⇒ 【Python】SARIMAモデルによる時系列予測をやってみる




コメント