金融時系列において、しばしば観察される現象として時系列の変動が大きくなるとしばらく変動の大きい時期が持続し、変動が小さくなるとしばらく変動の小さい時期が持続するというものがあります。(ボラティリティ・クラスタリング)
ここでいう変動とはボラティリティの事であり、モデルでいうと誤差項の部分当たります。ARモデルの派生形では、この誤差項の部分はホワイトノイズである(ボラティリティは常に一定)としており、金融市場でじばしば観測されるボラティリティの変動を説明することができません。
そのために開発されたモデルが、今日紹介するボラティリティ変動モデル(ARCH・GARCH・SV)と呼ばれるものです。これら特徴としては誤差項の分散に時系列依存構造があるとしている点です。
ARCHモデルとは?
ARCH(アーチ,AutoRegressive Conditional Heteroscedastic)モデルとは、金融経済学、統計学、計量経済学などにおいて分散不均一性を示す時系列データに適用されるモデルで、日本語では、「分散自己回帰モデル」「分散不均一モデル」と呼ばれています。
なぜARCHモデルが重要なのかというと、前回紹介したARモデルはモデルを作ってそれを時系列データに当てはめ際の残差がホワイトノイズであれば、信頼性が高いということなのですが、実際に為替レートや株価などの金融商品の時系列データを分析すると、残差はホワイトノイズの性質を満たしていないことが結構あります。
その場合、その金融商品価格の時系列データの残差の分散は一様ではなくばらつきに特徴がある、つまり「分散の不均一性(heteroscedasticity)」があるという事になります。
このような「分散の不均一性」を組み込んだ時系列モデルがARCHモデルです。ARCHモデルでは、今期の分散が過去の分散に依存することをモデルに組み入れます。これが「分散不均一の自己回帰過程(ARCH)」の意味です。
このまま説明すると、分散?不均一?と脱落していく人がかなり多いので、まずはAR(1)モデルの誤差項を入れ換えてARCHモデルを説明していきます。
AR(1)の時系列モデル:r(t) = r(t-1) + e(t) ※e(t)はホワイトノイズ
ARCHモデルでは上のe(t)はホワイトノイズではなく、以下のu(t)で置き換えます。
r(t) = r(t-1) + u(t)
u(t) = v(t) SQRT(a0 + a1 u(t-1)²)
ここで、v(t)は平均0,分散1のホワイトノイズ(標準正規乱数)になります。そして、a0 > 0 ・ 0 < a1 < 1 ・ SQRTは√(平方根)を意味します。
上のモデルでは、分散が1期前の分散に依存するのでARCH(1)といいます。また残差の2乗は1期前の残差の2乗に依存するということを表しています。一応、a0=1 and a1=0 のとき、ARCH=ARとなります。
株価収益率などの金融資産時系列データの分散の不均一性を説明するモデルとしてはARCHモデルよりも、後述のGARCHモデルの方がすぐれていることが証明されているので、ARCHに関してはこんなのもあるんだ程度の認識でいいと思います。
GARCHモデルとは?
先ほど説明したARCHモデルを拡張したのがGARCH(ガーチ,Gereralized ereralized ARCH)モデルです。
このモデルは、ARCHモデルの条件付き分散が過去の分散だけでなく過去の残差の2乗にも依存するという関係を組み込みました。
ARCHからGARCHへの発展は、AR→ARMAの流れと同じ感じです。GARCHモデルは下のように定義されます。
y(t) = y(t-1) + u(t)
u(t) = v(t) SQRT(h(t))
h(t) = a0 + a1 u(t-1)²+ b1 h(t-1)
ここでARCHモデルと違っている点は、a0 > 0 ・ a1 + b1 < 1 ・ u(t)はホワイトノイズではなく、v(t)がホワイトノイズになります。
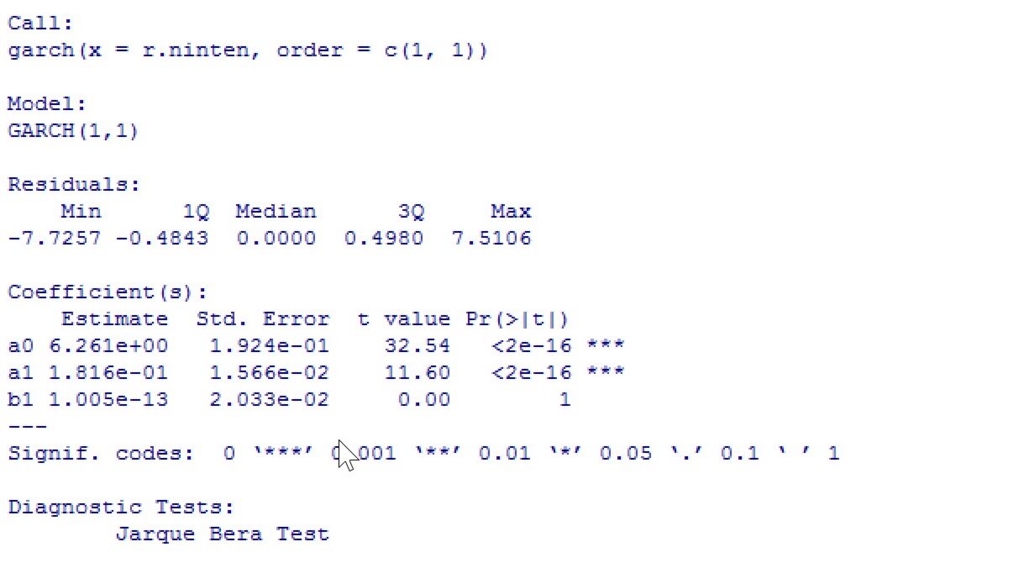
GARCHモデルはRにも計算用の関数が既にあり、ARCH(q)モデルもGARCH(0,q)モデルとなるので、garch()をつかってRで推計することができます。
次は実際にRで、ARCH・GARCHモデルの検証を行っていきます。
関連記事:【R言語】株価データへのGARCHモデルの当てはめ
ちなみに、時系列分析については、この本がとても分かりやすかったので、もし時系列分析でつまずいている人は是非一度読んでみてください。
現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~


コメント