Pythonでビットコインの価格データを時系列分析する手順と方法を解説

Contents

時系列データ分析の概要
ビットコインの価格データを入手する
価格データをMatplotlibで視覚化する
差分と変化率を計算する

トレンド(傾向変動)とは何か？

時系列データ分析の概要

今回はデータ分析初学者向けに、時系列データ分析の基本的な手順をビットコインの価格データを使って行っていきたいと思います。普通のデータ分析が身長体重のようなことなる2つの変数の関係性を分析するのに対して、時系列データ分析は現在のデータが過去のデータとどう関係があるのかを分析し、そこから未来を予測する分析手法です。

株初心者が本気で儲けるブログ

【統計学】時系列データ分析の考え方

https://dmjtmj-stock.com/entry/2017/01/20/000251

時系列データとはなにか？時系列データとは、時間の推移とともに変化していくデータであり、その順序におおきな意味を持つことが特徴です。時系列データは経済やファイナンスの分野で、観測されることが多く、『為替レート』、『株価データ』などが代表的な時

今回のビットコインの価格データを分析する場合ならn日目のビットコインの価格はn-1日・n-2日目のデータとどう関係があるのかを分析するといった感じです。

ビットコインの価格データを入手する

分析においてまず大切なのはデータ集めです。ビットコインの価格データの入手方法については以下の記事で取り上げたのでそちらを参考にしてやります。

参照：Pythonで自動売買Botを作る②～仮想通貨取引所からビットコインの価格を自動取得する

参照：【Python】CoinGeckoのAPIでビットコイン・アルトコインの価格データを取得する

これで分析のもとになる価格データは入手できたので本題の時系列データ分析に移ります。

#### ビットコインの価格データを取得する #####
# ライブラリの読み込み
import pandas as pd
import time
import matplotlib.pyplot as plt
import datetime
import requests
import json
import numpy as np
import talib
%matplotlib inline

#ビットコインの価格を取得する関数 
def get_bitcoinprice(): 
    url = 'https://api.coingecko.com/api/v3/coins/bitcoin/market_chart?vs_currency=jpy&days=max' 
    r = requests.get(url) 
    r = json.loads(r.text) 
    bitcoin = r['prices'] 
    data,date = [],[] 
    for i in bitcoin: 
        data.append(i[1])
        date.append(i[0])
    bitcoin = pd.DataFrame({"date":date,"price":data}) 
    price = bitcoin['price']
    date_shape = []
    for i in bitcoin['date']:
        tsdate = int(i / 1000)
        loc = datetime.datetime.utcfromtimestamp(tsdate)
        date_shape.append(loc)
    price.index = date_shape
    del bitcoin['date']
    return bitcoin

price_data = get_bitcoinprice()

#　先頭部分を表示
price_data.head()

↓みたいなデータが返ってくれば成功です。

価格データをMatplotlibで視覚化する

まずデータ分析の基本は取得した価格データの大まかな特徴を把握するために視覚化します。PythonのMatplotlibでデータを視覚化（プロット）する方法は「df.plot()」と「plt.plot()」の2パターンがありますが、ただ視覚化するだけならどちらでも構いません。

参照：【Python】Matplotlibでのグラフ作成の基本をわかりやすく解説する

#ビットコインの価格データを可視化する
ax=pd.Series(price_data['price']).plot()
ax.set_title('Price Changes Of Bitcoin') 
plt.show()

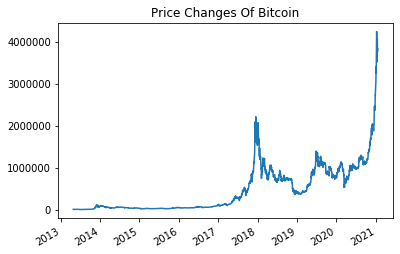
こんな感じで視覚化できました。にしてもすごい値動きですね。

差分と変化率を計算する

時系列データ分析において大事なのは当日と前日の価格差です。つまりn日の価格はn-1日と比較してどれだけ変化したかという差分と変化率を考えることが重要になってきます。Pythonにおける差分の計算は.diff()、変化率の計算はpandasに用意されているpct_change()で簡単に計算できます。

# 差分を計算する
price_data['price'].diff()

また後ろに.plot()を付けるとそのまま視覚化もできます。

#差分を計算して結果をプロットする
price_data.diff().plot()

差分をざっと取っても大きな価格変動が起こっているのが伺えますね。一応変化率も計算して、同じようにプロットしてみます。

# 価格データの変化率を計算する
price_data['price'].pct_change()

# 変化率を計算して結果をプロットする
price_data['price'].pct_change().plot()

変化率でみても、日次で最大40％もの変動が起きており、株式市場なんかと比べると半端じゃないボラティリティがあることがグラフで視覚化すると一目瞭然で分かります。そして、通常のデータ分析と時系列分析の少し違う点はまずこの差分と変化率の計算するという点でしょう。

また今回のように変化の幅が大きい場合は対数変化率にして計算することもあります。また株価や為替などの金融データの場合は変化率を収益率と呼ぶこともあります。

トレンド(傾向変動)とは何か？

そして時系列データ分析において大切な要素は「トレンドの把握」です。これはほかのデータにはない処理で、時系列データ分析独特の処理です。

「トレンド(傾向変動)」というのは、株式市場などの金融市場において、価格が一定期間継続して上昇または下落する動きのことを指します。金融市場におけるとトレンドは大きく分けて「確定的トレンド」と「確率的トレンド」2種類が存在していると言われています。

まず「確定的トレンド」というのは、経済成長や景気などの社会的要因と密接な関係があると言われており、季節変動やバブルなどはこの「確定的トレンド」に分類されます。要は金融政策や地震・干ばつなどの天変地異によって発生する価格変化の傾向という感じです。

そして「確率的トレンド」というのは名前の通りランダムに発生するトレンドのことを指します。要はランダムウォークのことです。

トレンドを判定する

トレンドを把握するのに必要なデータは以下の5つです。

価格データの対数

価格データの変化率

価格データの対数変化率

価格データの対数差分

価格の差分

ここで新しく登場した要素として対数データ・対数変化率・対数差分というものがあります。これらは価格データ・変化率・差分を対数(log)を取って計算したものです。

価格変動を長期で見る場合は対数を取ってみることで変化率をどの価格帯でも同じスケールで見ることができるので、基本的に価格データは対数を取って分析することが多いです。

日経平均も1949年から見れば100倍ですし、ビットコインも最大200倍近く価格が上昇しているので、時系列データの中でもこういった変化率が馬鹿みたいに大きい時系列データは対数を取って計算した方が良いです。そして、Pythonでビットコイン価格データを対数に変換しなおす場合は、numpyの「np.log()」という関数を使用します。