【R言語】株価データへのGARCHモデルの当てはめ

前回までのあらすじ

https://tkstock.site/2017/04/03/2017-04-03-000000

今回はRでARモデルを作って検証していきます。一応ARモデルについておさらいしておくと、自己回帰モデルとはその名の通り、過去の自分のデータと回帰する分析手法のことを意味します。これは色々ある時系列モデルの中で一番理屈が簡単なモデルで他のモデルの基礎にもなっています。そして、１期前のデータだけから回帰したARモデルをAR(1)と表します。同様にp期前までの全てのデータを使って今日のデータを予測するモデルはAR(ｐ）モデルと書きます。・使うデータ2005年から2016年までの任天堂の株価収益率のデータ(※今回は...

前回のARモデルに当てはめ、その残差分析を行ったところ任天堂の株価収益率のデータには分散不均一性があることが分かりました。

というわけで今回は、引き続きRを使って分散不均一性を説明しうるモデルであるGARCHへの当てはめを行っていきたいと思います。

GARCHモデルについては↓

Rによる時系列データのGARCHモデルへのあてはめ

・今回は使うRのパッケージ

tseries・TSA・fGarch・forecast

（インストールされていない場合はinstall.packages(””)でインストールしてください）

まずlibrary(パッケージ名)で読み込みます。

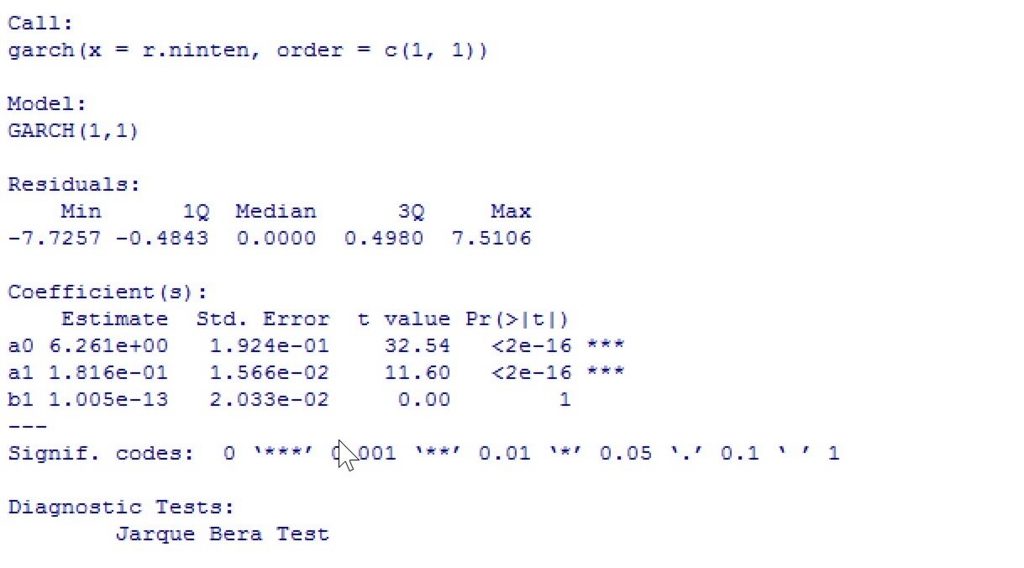
# GARCH(1,1)モデルの任天堂株価収益率データへの当てはめ
g.ninten <- garch(r.ninten,order=c(1,1))
summary(g.ninten)

order=c(p,q)、p はσ²t-i 、q はσ²t-iの項の次数。r.ninten=任天堂の株価収益率が入っている時系列データのオブジェクトです。

実行すると下のような結果が出力されます。

この結果は下のような推定式になるという事を示しています。

推定式：σ²t＝ 6.261 ＋ 0.1816σ²t-1＋1.005×10⁻¹³ε²t-1

そして、この推定式の信頼性の検定のためにJarque Bera 検定と Box-Ljung 検定も一緒に行ってくれています。

↓分析結果

Diagnostic Tests:
Jarque Bera Test

data: Residuals
X-squared = 3998.7, df = 2, p-value < 2.2e-16

Box-Ljung test

data: Squared.Residuals
X-squared = 2.3333, df = 1, p-value = 0.1266

一応、推定した時系列モデルが当てはまっているかの判断基準としては、係数を検定した分析結果のP値の大きさを見ることが大切です。

jarque.bera（ジャックベラ）検定とは、標本データが正規分布に従う尖度と歪度を有しているかどうかを調べる適合度検定、つまり正規性があるかどうかの検定です。ここではｐ値が非常に低いので正規性は棄却されることになります。

Ljung-Box test は残差系列の２乗とラグ１についての Ljung-Box 検定（時系列データが自己相関関係を有しているかどうかを調べる検定）の結果が表示されています。（ちなみに2乗した値を使うのは、GARCH がεtの分散の時系列の動きについてのモデルだからです。）

しかし、検定統計量であるχ2分布の自由度 k-p≧１となるラグ次数以外は意味がありません。今回は係数が３つあるので、パラメータ数 p=3 であり、ラグ次数 k≧4 で有意となるということを示しています。

結論としてモデルの係数のP値は低く、信頼性が高いが残差を検定したところ正規性がないので当てはめとしては不十分という事になります。

時系列分析については、この本がとても分かりやすかったので、もし時系列分析でつまずいている人は是非一度読んでみてください。

現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~

横内大介,青木義充技術評論社 2014-02-18