【金融工学】ポートフォリオ理論とCAPM

 

 

今回はファイナンスにおける債権のリスクの計算方法の一つであるCAPM理論について取り上げていきたいと思います。

 

 

まず今２つの証券ABを保有しているとします。そして、A・Bそれぞれの収益率：rA,rBは平均：μA,μB、分散：σA,σBの確率分布の実現値とします。そして２つの共分散をσABと表します。

 

 

確率分布？共分散？となってしまう方は↓の記事を見ていただけると理解できると思います。

【統計学】確率変数・確率分布の分かりやすい説明

【統計学】 共分散と相関係数の簡単な説明 

 

 

今この２つの証券でポートフォリオを組むという事はそれぞれの証券をs：tの割合で保有するという事になります。（s+t＝１）

 

 

手数料などは考慮しないとするとこのときの月次収益率：rは、r＝s×rA+t×rBで算出されます。このrをポートフォリオ収益の確率変数からの実現値と考えれば、ポートフォリオの確率変数は平均と標準偏差は期待リターンとリスクを表しているという事になります。そして、このポートフォリオの期待収益率とリスクを式で表すと、下のようになります。

 

 

E(R)＝ s × μA + t × μB

SD(R)＝ √s²σ²A + t²σ²B + 2st σAB

 

 

上でも述べたようにσABは２つの証券ABの共分散であり、この値はAとBの相関関係が強いほど数値が大きくなります。なのでAとBの相関関係が小さいほどリスクの値は小さくということになります。

 

 

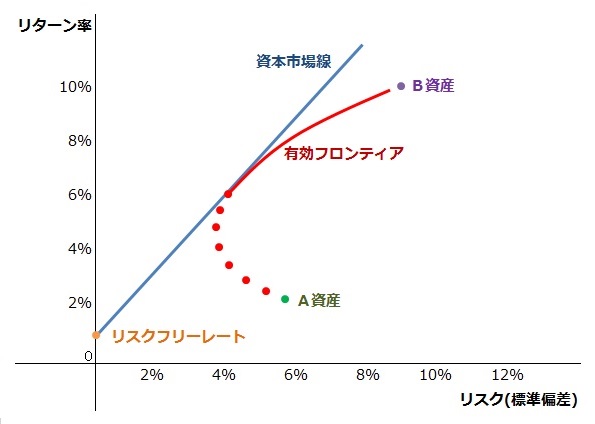
そしてこのE(R)とSD(R)とs+t＝１を連立し、そのリスクとリターンの関係の軌跡を図で表すと下のようになります。

 

参照:http://words.equity-investment.info/portfolio.theory.html

 

 

下半分の点線になっている部分は、リスクの方がリターンよりも高くなっているので、無視します。つまり大切なのは上の部分でこのカーブの事を効率的フロンティアと言い、かのカーブの上で最も分散（リスク）の小さいポートフォリオを最小分散ポートフォリオと言います。

 

 

次に効率的な部分の中でより効率の高い部分の絞り込みに入るわけですが、このカーブだけでは決まることができないので、無リスク資産の金利を使います。無リスク資産のポートフォリオは（0、r）※rは無リスク金利を切片した直線（資本市場線）で表すことができます。資本市場線の計算は難しいのでここでは省略します。

 

 

ここで市場が、参加者が常に同じ価値観のもと効率的に行動し、証券の情報は常に株価に織り込まれる効率市場仮説であると仮定した場合、接点ポートフォリオは市場ポートフォリオ（全ての証券を時価総額の比率で購入したポートフォリオ）と一致します。

 

 

そしてこの理論を1つの証券に当てはめた場合、その証券の期待収益率：E(R)は下のような式になります。

 

E(R)＝ r + β ( E (Rm) ー r )

 

 

rは無リスク資産の金利、E(Rm)は市場リターン、βはβ値を表しています。

【金融工学】 β値（ベータ値）とは？

 

 

そして、このβを推定するために使われるのが、線形モデル（回帰分析）の考え方です。具体的には個別証券の収益率(y)とインデックス指数の変化率(x)を回帰分析し、y＝βx+αの β の部分がβ値とされます。

 

このCAPMによって計算された個別証券の期待収益率は、企業価値の算出においてはその証券に投資することで期待される収益（株主の期待収益率）であることから、株主資本コストの値とされます。

 

 ↓の本は、こんな感じで証券のリスクリターンの数値化などについてできるだけ分かりやすく説明しているのでもし興味があればどうぞ