株式投資やマージャンや競馬をする上において、確率についての理解を深めることはとても大切です。なぜかというと麻雀は確率のゲームですし、株式投資では、リスクの大きさを確率で表すことでポートフォリオを作成しますし、株価の変化率も確率で考えることが可能だからです。
もし株式市場を始めとする、金融市場で勝って生き残りたいのであれば、統計学は絶対に必要な知識であると私は思います。そういうわけで、今回は統計学において非常に重要な定理である「大数の法則」と「中心極限定理」について説明していきたいと思います。
大数の法則とは?
まず『「大数の法則」とは、ある母集団から無作為抽出された標本平均は標本の数をどんどん大きくしていくと、その分真の平均に近づいていく』という法則です。
そして、標本サイズが無限大になったとき、標本の平均が母集団の平均に一致する性質のことを『一致性』と言います。
具体的にどういうものかというと、コイン投げをする場合、その試行回数を増やしていけばいくほど表の出る確立が理論上の確立である1/2に近くなるなど、『大数の法則とは、数多くの試行を重ねる(標本数を増やす)ことにより事象の出現回数が理論上の値に近づくという定理』です。
この「大数の法則」をもう少しわかりやすくいうと、短期間の結果をみると確率的にはありえない不思議が起きたとしても、十分回数を重ねると数学的な確率に近づくということです。
# さいころの目のシュミレーション
index = []
dice_data = []
for i in range(1, 8):
n = 10 ** (i)
index.append(n)
dice_data.append(np.random.choice(range(1, 7), size=n).mean())
pd.DataFrame(dice_data, index=index, columns=['さいころの目の平均値'])
# 対数の法則
means, numbers = [], np.array([])
for i in np.random.choice(range(1, 7), size=500):
numbers = np.append(numbers, i)
means.append(numbers.mean())
plt.plot(means)
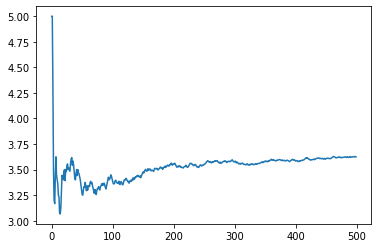
さいころの理論上の平均である3.5に収束していっているのが分かります。
中心極限定理とは?
一方「中心極限定理」とは 、標本の平均と母集団の平均との誤差についての定理で、n が大きければ大きいほど、標本の平均と真の平均の差の作る分布は、平均 0、分散 σ²/n の正規分布に近づくという定理です。
もし母集団の分布が、どんな分布であっても、標本平均と母集団の平均の誤差は、標本の量(サイズ)を大きくしていくと、正規分布に近似していきます。つまり『標本の大きさを大きくしていくと標本平均の分布は正規分布の近似できるという法則です。』
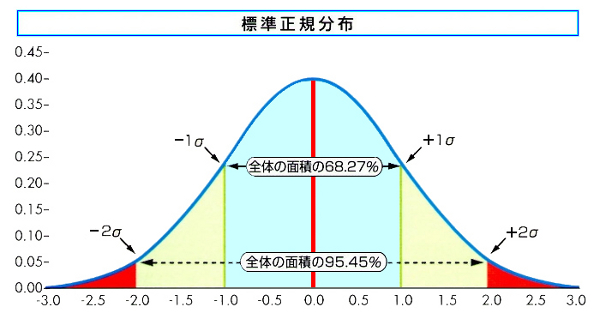
※正規分布(ガウス分布):平均付近が一番高くて、平均から離れるにつれてだんだん低くなっていく、ほぼ左右対称な釣り鐘型の分布のこと。この世でもっとも一般的な分布と言われており、さまざまな社会現象や自然現象に当てはまる確率分布です。母集団の性質がわからないときなどはとりあえず正規分布だと仮定して計算したり統計学において超超重要なものです。(詳しくは【統計学】正規分布とは?を参照)
統計学を勉強すると、この2つは一見同じことを言っているようでそうではなかったりと、勉強していく上で皆が1回は疑問に思うポイントなのですが、イメージとしては、データ数が多くなると、「大数の法則」により、標本の平均と母集団の誤差は小さくなる(標本平均の値は母平均の値に近づいていく)、そして中心極限定理によって、標本平均の分布は正規分布に近づいていくというように感じです。若干似ているんですけどちょっと違うんですよね・・・紛らわしい・・・。
これらの法則がなぜ大事なのかというと、正規分布による推定や検定の大前提になるからです。これによって標本数が大きいものは正規分布の従うと仮定することが出来ます。これを『正規近似』といいます。特に統計検定二級の問題なんかでは二項分布を正規分布だと近似して推定や検定も問題を説かせるパターンが多いです。
次は検定や推定で使用する標本分布の性質と使いどころについてみていきます。

コメント