【分かりやすい統計学】 ⑧標準正規分布による確率計算と分布表の見方

Contents

前回の復習～標準化と標準正規分布
確率とは分布の面積である
分布表の見方
標準正規分布による確率計算
例題で(標準)正規分布の確率計算を理解する

前回の復習～標準化と標準正規分布

標準正規分布について軽く説明したところで、標準正規分布を使った確率の計算のやり方を解説していきます。前回の復習ですが、標準正規分布とは、正規分布の確率変数を一定の式にし、確率密度関数を簡単な形にしたもののことをさします。

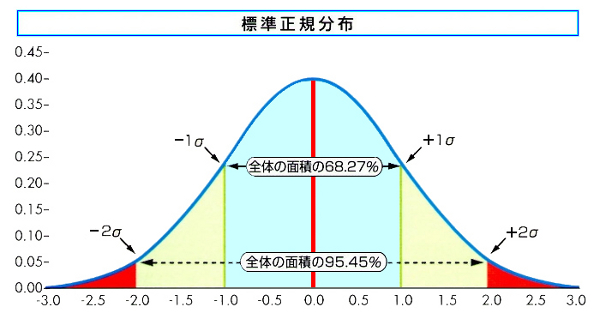
標準正規分布の特徴としては平均が0、標準偏差1になります。そして、標準正規分布は下のような分布となります。

(参照:https://wizard-fx-trader.com/bollinger_band/)

※平均（μ）＝０、分散（σ²）＝１

確率とは分布の面積である

そして、標準正規分布を確率計算においてどう役立てていくかという話ですが、⑤確率変数でも解説したように、『統計学において事象の確率は、分布における面積で表現されます』これが標準正規分布にも当てはまり標準正規分布における確率の事象はｘ軸に対応する面積の大きさで表すことができます。

『標準正規分布は平均０分散１なので、確率計算が非常に簡単』であるために重宝されます。なので『正規分布の事象の確率計算では、絶対といっていいほど標準化によって標準正規分布に変換する作業が行われます。』

そして、標準正規分布で表せる数値は基本的にいちいち計算する必要はなく、すでに計算されたものが数値表になっており、正規分布を使用した統計的仮説検定などで使用されています。これを『分布表』といいます。

分布表の見方

さて分布表の見方ですが、まずこの『分布表の中の数値は何を表しているのかというと、統計量Zに対応する分布の面積、つまりは事象の確率』です。

確率計算の手順としては、標準化で統計量Zを計算→分布表からZに対応する面積（確率）を算出する、という流れになります。

標準正規分布の分布の面積の合計は１なので、分布表の中の数値は最大で１です。そして、正規分布は左右対称であるため、分布の半分の面積は0.5です。もしZ値がマイナスになった場合でも左右対称であるので、面積は+のものに対応する数値と同じです。

分布表は統計検定二級で配られるものであれば上側確率を書いたものであったり、ものによって形式が異なる場合がありますが、基本的に書いている内容自体は確率の面積であり同じです。

標準正規分布による確率計算

確率変数X（あるデータ）を標準化した統計量Zに対応する確率(P)の求め方は下のようになります。

・確率変数Xを標準化したZが0.62よりも小さくなる確率を求めるとき

数式ではP(Z < 0,62)と表現されます。これを確率分布の面積で表現するならば、以下のような感じになります。

Z＜0.62となる確率を知りたい場合は上の図の塗られた部分の面積を計算すればいいということになります。ここで先ほどの分布表を使用します。

知りたい標準正規分布の面積P(X)の数値は、Z＝0.62に対応する部分、つまり標準正規分布表のz = 0:6 の行と0:02 の列の交点なので、0,2324となります。そして、分布の半分の面積は0.5であるので、Z< 0,62となる確率は0.5＋0.2324＝0.7324≒約73％ということになります。

・確率変数Xを標準化したZが、－0.62≦Z≦0.62の範囲になる確率を求めるとき

これを数式で表すと『P(－0:62 < Z < 0:62)』となります。確率計算のやり方は考え方自体は先ほどと同じです。正規分布は左右対称であること、面積の合計１で分布の半分の面積は0.5であることを押さえておけば頭の体操のようなものです。正規分布の面積は左右対称なので、Z値がマイナスの場合でも同じように考えることができます。

P(－0:62 < Z < 0:62) = P(Z < 0,62) － P(Z < －0,62) = 0,7324 －（0.5－0.2324） = 0,4648

この変換は図で示すとわかりやすいです。

今度は逆にP(-a ≦ Z ≦ a) が0,5 となるaを求めたいとすると上図の斜線部分（全体の面積の50 ％）の両端に位置するz 座標が知りたい場合は両側なので、片側25 ％ずつということで、P(Z ≦ z) ＝ 0,75 　のようなaを探すと早いです。左側でも問題なのですが、分布の右側で探すのが一般的です。

0,75 に１番近い数字を探す　→　0,67 と0,68 の間ということになります。以下の範囲は推定や検定の信頼区間としてよく出てくるものです。

P(－ 1,65 ≦ Z ≦ 1,65) 　→ 　0,90
P(－ 1,96 ≦ Z ≦ 1,96) 　→　0,95
P(－ 2,58 ≦ Z ≦ 2,58) 　→ 　0,99

まあこれだけだとイマイチ正規分布の確率計算の手順が理解できないと思うので、次では実際に、例題を解いていくことで確認していきます。

例題で(標準)正規分布の確率計算を理解する

例題

20歳男子の身長は平均170cm、標準偏差8の正規分布に従うことが分かっている。

問１：この時、身長180cm以上の20歳男子はどれくらいの割合を占めるか？

＜解き方＞

この場合だと計算したい確率変数X(あるデータ)とは、身長が180㎝以上ある男子の割合です。身長の確率変数Xを先ほどの標準化の式に当てはめて標準化します。

問題分から20歳男子の平均身長は170、標準偏差が8とあるので、それぞれμ＝170、σ＝８だとわかります。そして、今回知りたいのは、20歳男子の中で身長が180㎝以上ある確率なので、確率変数X＝180となります。

これらの数値を正規分布の標準化の式に当てはめると

Z＝（180－170）/8＝1.25

となります。

次はこのZの数値を先ほどの正規分布の分布表と照らし合わせます。

この分布表からZ＝1.25に対応する、分布表の値は0.3944となります。

そして、合計１で左右対称の正規分布の半分の面積は0.5なので、身長が180未満の割合は0.5＋0.39＝0.89≒89％なります。なので、逆を考えて身長が180㎝以上の20歳男子の割合は100ー89＝約11％であるとわかります。

今回は理解していただくために、回りくどい方法で計算しましたが。別解としてはそのまま上側確率を求める方法でもいいです。

標準化してZ＝1.25に対応する、分布表の値は0.3944とわかる→分布表の半分の面積は0.5なので、180㎝以上の確率（Z＞1.25の確率）0.5ー0.3944＝10.56≒11％

問１：この時、身長165cm以下の20歳男子はどれくらいの割合を占めるか？

まずは先ほどと同じように標準化します。まずμ＝170、σ＝８だとわかります。そして、今回知りたいのは、20歳男子の中で身長が165㎝以下である確率なので、基準となる確率変数X＝160となります。

これらの数値を正規分布の標準化の式に当てはめると

Z＝（165－170）/8＝⁻0.625

となります。Z値がマイナスの場合でも正規分布は左右対称なので、問題ありません。絶対値として、先ほどの正規分布の分布表のZ=0.625≒0.63の部分と照らし合わせます。すると対応する面積の値は0.2357となります。

この0.2357は以下の図で表される部分の面積なので、先ほどの正規分布の片側全体の面積が0.5である性質を利用して、身長が165㎝以下の20歳男子の確率（Z<0.63）である確率は、0.5－0.2357＝0.2643≒26.4％だとわかります。

まとめ

以上が正規分布（標準正規分布）を使用した確率計算の方法と分布表の見方です。

①：求めたデータを正規分布である場合、平均と分散・標準偏差を求める

↓

②：その正規分布を標準正規分布に変換→確率変数XをZへと標準化

↓

③：分布表からZ(標準化変換した確率変数X)に対応する面積（確率）を把握し、分布全体の面積が１、片側全体の面積が0.5である正規分布の性質を利用して状況（〇〇以下or〇〇以上）に対応する面積（確率）を計算する

という感じです。