t検定とは?
これまでは母集団のデータの性質である母平均と母分散が分かっているパターンにおける検定・推定を行ってきましたが、今回は母集団の平均が未知である場合の推定・検定(t検定)について説明していきます。
標本平均 X を標準化した変量の分布は、母集団が正規分布であるか、標本サイズが十分に大きい場合は、中心極限定理により正規近似され、 と表すことができます。
と表すことができます。
ここで、N(0,1) の標準正規分布に従う変数 z が(−1.96 ~+1.96) の間をとる確率は 95 %であることから下のように変形することができます。

つまり、これは未知の母平均 µ が区間 ( X −1.96σ/√n≦μ≦X+1.96σ/√n) にある確率が 95 %であるということを表しています。
ですが、母平均 µ の値が未知なのに 母分散σの値が既知であるということは、まずあり得ないので、この区間は計算できないことがほとんどです。
そういう時に使われるのがt検定というやつです。母標準偏差 σ の代わりにその推定値、標本標準偏差 S の平方根√Sの数値を代入して![]() を計算します。
を計算します。
しかし当たり前ですが母分散σの代わりに、少ない母数の標本から算出した数値である標本分散の値を使っているので、データ数が少なければ少ないほどZとt数値の誤差は大きくなってしまうので、自由度 n−1 の t 分布とします。

この t 分布は自由度によって形が大きく変化します。正規分布のグラフの形を作るパラメータが平均と分散であったように、t 分布におけるグラフのパラメータは自由度 k です。
t分布の特徴としては、原点に関して左右対称で、正規分布よりも裾が厚いことがあります。そして自由度 k が大きくなる程、裾は薄くなり、正規分布に近似していきます。自由度 k = ∞のとき、t 分布は標準正規分布 N[0,1] となります。
 (参照:テクノビジョン ダイジェスト)
(参照:テクノビジョン ダイジェスト)

t分布の確率計算
t 分布表は、基本的に X > 0 のとき (右裾) の数値しか載っていません。
例:X ∼ t7のとき P(X < x) = 0.99 となる x を求めよ。
解答:
P(X < x) = 0.99 ということは、P(X > x) = 1−0.99 = 0.01 であるような x を求めればよい。 t 分布表: 自由度 df = 7 の行、右裾確率 p = 0.010 の列に対応する値は x = 2.298となります。
終わり
統計学についてしっかり勉強するのであれば、↓の本が分かりやすく説明していてオススメです。
→【わかりやすい統計学】 ⑬ベルヌーイ試行と二項分布について
→PythonでデレステでSSRを引くまでの課金額を計算してみる
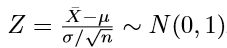


コメント