こんにちは、ミナピピン(@python_mllover)です。今日はPythonで時系列モデルの一種であるARモデルを実装して時系列データ予測をしてみたいと思います。
ARモデルの特徴
・定常過程でしか使用できない
⇒ 【Python】「ADF検定」で時系列データの定常性・単位根を確認する
使用するデータ
お馴染みの航空データのあれです。アイスクリームの売上データと同じで周期性が明確なのでサンプルにはうってつけです。
# ライブラリをインストールする $ pip install pydse
# ライブラリの読み込み import numpy as np from pydse import data %matplotlib inline df = data.airline_passengers() df.plot()
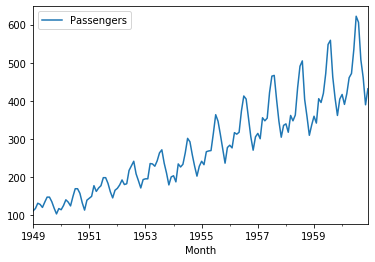
ARモデルでの時系列分析をPythonで実装する
# 変化率を計算する
df['change'] = df['Passengers'].pct_change()
from statsmodels.tsa import ar_model
for i in range(20):
model = ar_model.AR(df['change'][1:])
maxlag = i+1
results = model.fit(maxlag=maxlag)
print(f'lag = {i+1}, aic : {results.aic}')
<実行結果>
lag = 1, aic : -4.446973357475064 lag = 2, aic : -4.4631716863118545 lag = 3, aic : -4.447775449486837 lag = 4, aic : -4.547186384494698 lag = 5, aic : -4.535533168461425 lag = 6, aic : -4.52194132402394 lag = 7, aic : -4.544234892748647 lag = 8, aic : -4.838737433463194 lag = 9, aic : -4.862897005884629 lag = 10, aic : -5.369470828101987 lag = 11, aic : -5.667943927077143 lag = 12, aic : -6.097118563657251 lag = 13, aic : -6.15443976125231 lag = 14, aic : -6.146411714225788 lag = 15, aic : -6.149795460174459 lag = 16, aic : -6.143571088872173 lag = 17, aic : -6.145833721785127 lag = 18, aic : -6.144051613542763 lag = 19, aic : -6.122643951390369 lag = 20, aic : -6.125921513035268
時系列モデルのラグの次数はAIC(赤池情報量規準)を見て選択します。AICが最小になるモデルが最適なモデルという事になります。基準尺度にはAICの他にもBIC(ベイズ情報量規準)というものも存在しています。
ラグ13の時にAICが最小となっているので、今回はAR(13)とします。
次にモデルの当てはまりの良さを確認するために残差を算出してプロットします。
model = ar_model.AR(df['change'][1:]) result13 = model.fit(maxlag=13) # 残差 resid13 = result13.resid #残差プロット plt.bar(range(len(resid13)), resid13)
続いて自己相関係数も確認してみましょう。
from statsmodels.graphics import tsaplots tsaplots.plot_pacf(resid13, lags=40)
見て分かるようにほとんどが95%の有意水準に収まっていることがわかります。
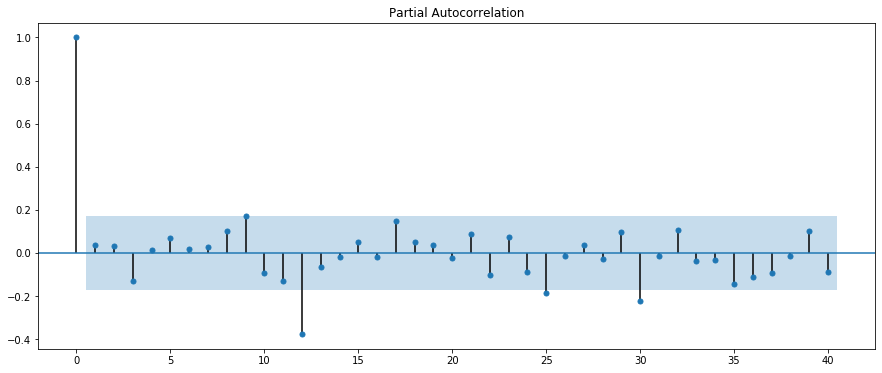
ARモデルで時系列予測
train = df['change']['1949-02-01':'1953-12-01']
test = df['change']['1954-01-01':'1958-12-01']
from statsmodels.tsa.ar_model import AR
ar = AR(train).fit(maxlag=20, ic='aic')
# モデルに当てはめて予測する
ar_predict = ar.predict('1954-01-01', '1958-12-01')
plt.plot(test, label='observation')
plt.plot(ar_predict, '--', label='forcast')
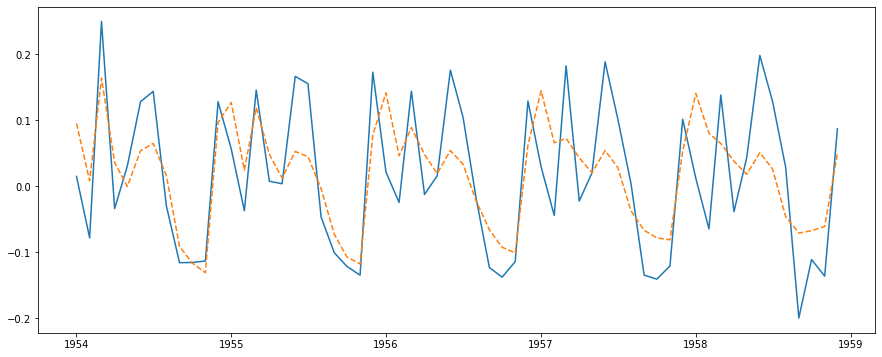
傾向は予測できていますが、スパイクについていけていない印象です。
⇒ 【Python】MAモデルによる時系列予測をやってみる
⇒ 【Python】VARモデルによる時系列予測をやってみる
⇒ 【Python】ARIMAモデルによる時系列予測をやってみる
⇒ 【Python】SARIMAモデルによる時系列予測をやってみる



コメント