前回までのあらすじ
引き続き確率変数関連について解説していきます。というわけで今回は確率密度関数について説明していきます。
確率密度関数とは?
前回の具体例で出てきたサイコロは確率変数X(とりうる値の範囲)が、1から6で、取る数字が1,1やら2.222といった細かい値にならず、とりうる数字が1,2,3,4,5,6の6通りしかない、いわゆる離散型確率変数でした。(この辺がイマイチ分からないという方は上の記事でより詳しく解説しています。)
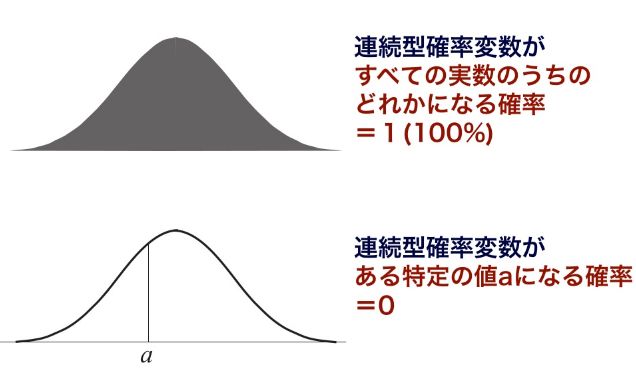
ですが、実際に統計分析を行うと、離散型よりも連続型のほうが、圧倒的によく出てきます。なので、 X=aとなる確率には、あまり意味がありません。
連続型確率変数で大事なのは、『特定の数値になる確率よりも、一定の範囲の数値になる確率』です。まあ特定の値になる確率を求めようにも、連続分布において、特定の値にちょうど一致する確率は 0 なので不可能ですが…。
これをもうすこし分かりやすくするために、株価の例にとって説明すると、日経平均が、18568円ちょうどになる確率を求めることよりも、18000円~20000円の範囲になる確率を求める方が大事だということです。

参照(http://www.slideshare.net/akiraasano/2014-2014-12-3)
というわけで連続分布の場合、Xは特定の値を取る確率ではなく、値に幅を持たせて、a≤X≤bとなる確率と考えます。
そして、『連続型確率変数の曲線を数式で表したものを確率密度関数』をいいます。 確率変数X が、a以上b以下( a≦X≦b)となる確率は面積で考えます。ここで高校の時に習った積分が登場します。

参照(http://www.slideshare.net/akiraasano/2014-2014-12-3)
面積を求める式は

となります。
これだけでは漠然としていて、???な人が多いと思うので、テストの点数で考えてみましょう。ここに10000人が受けて、平均が50点のテストがあり、得点の分布は次のような確率密度関数で表されているとします。

ちなみに縦軸の相対度数とは、ある数値が出てくる割合が全体の何%をしめるのかというものを表したものです。もし、ある数値相対度数が0.01ならば、その数値は1%の確率で出てくるということを表しています。
上のグラフならば、テストで35~40点を取る人の人数は相対度数が0.02なので、全体の受験者数の 0.02×100=2% ということを表しています。
次にこのこのテストで40点以下を取る確率が知りたいとすると、その確率は40点以下の相対度数の合計で求められるわけでその範囲は下のグラフのようになります。

この範囲の面積をどうやって求めるかというと、積分を使って求めるわけです。この分布を正規分布だとして計算すると、40点以下の相対度数の合計は0.160、つまり%で表すと16%になります。
統計分析において、確率密度関数は正規分布だと仮定して計算すると、計算がとても楽になり、この世界の事象のほとんどは正規分布であることが多いので、たいてい正規分布だと仮定して分析を行うことがよくあります。
ですが、株価の変動率などは正規分布より、※べき分布に近い動きをします。ならべき分布で、確率計算した予測モデルを作ればいいという意見もあるのですが、そうするとべき分布には平均分散といった統計量の概念がないので、株価の変動を表した確率密度関数をどうやって計算すりゃいいんだよっていう問題になるわけなんですよね・・・。
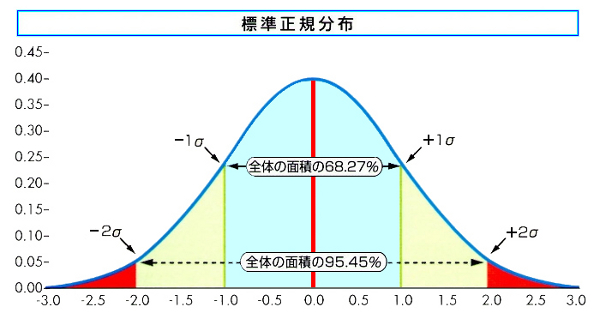
次は正規分布と標準正規分布を使った具体的な確率の計算方法について解説していきます。
追記:統計学の初歩的学習にはコチラの「マンガでわかる統計学入門」という本が分かりやすかったので紹介しておきます。

コメント