こんにちは、ミナピピン(@python_mllover)です。今日はPythonで時系列モデルの一種であるARIMAモデルを実装して時系列データ予測をしてみたいと思います。
使用するデータ
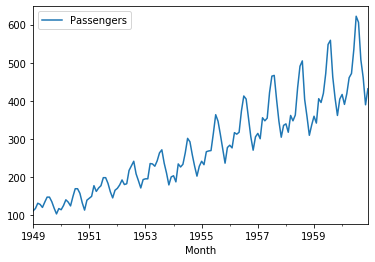
今回使用するデータはお馴染みの航空機の乗客データです。アイスクリームの売上データと同じで周期性が明確なのでサンプルにはうってつけです。
# ライブラリをインストールする $ pip install pydse
# ライブラリの読み込み import numpy as np from pydse import data import matplotlib.pyplot as plt %matplotlib inline df = data.airline_passengers() df.plot()
ARIMAのモデルの概要と特徴
ARIMAモデルは、データの差分を取ってARモデルと、MAモデルを統合したモデルです。ARモデルやARMAモデルはデータが定常過程であることが前提条件でしたが、このARIMAモデルは定常過程でないデータに対しても当てはめることが可能です。
そして、ARIMAには、下記の3つのパラメータがあります。
– p (number of AR terms) : 自己回帰の窓幅を何個前まで取るか
– q (number of moving average) : 移動平均の窓幅を何個前まで取るか
– d (number of differences) : 一次の差分か二次の差分か(季節以外の差)
ここで重要なのは、`p`と`q`の値をどのように決定するかです。片方が0だとそちら側もモデルの数値に反映されないので、p=0だとMA、q=0だとARモデルとできます。
ARIMAモデルを用いてデータ予測するためには、この3つのパラメータを適切に決める必要があります。 Pythonは、上記2.(差分を取る回数)は自動的に計算できないみたいなので、今回は差分回数は「1」で決め打ちします。
そして、pとqを決めるための指標にはACF(Autoorrelation Function)自己相関とPACF(Partial ACF)偏自己相関を使用します。
– p : ACFのupper confidential intervalがクロスするラインを選ぶ
– q : PACFupper confidential intervalがクロスするラインを選ぶ
from statsmodels.tsa.arima_model import ARIMA import statsmodels.api as sm print(sm.tsa.arma_order_select_ic(df['Passengers'], ic='aic', trend='nc'))
データはそのままのデータを使っています。そして結果から(4,2)が最適なpとqの組み合わせであることがわかりました。このパラメーターでモデルを作りましょう。
ARIMAモデルで時系列分析する
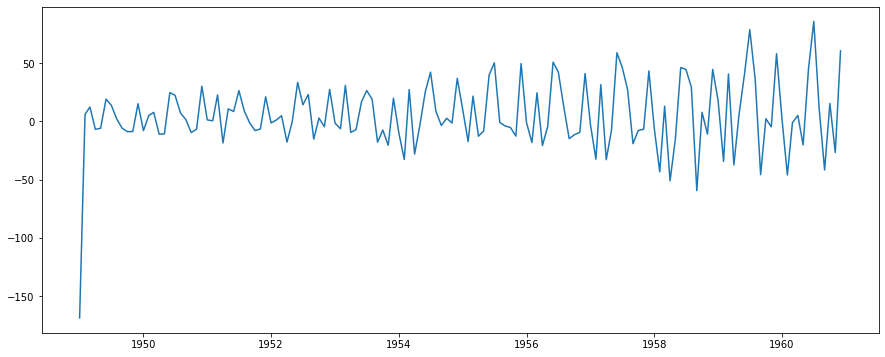
まずは残差をプロットしてみます。
arima_model = ARIMA(df['Passengers'], order=(4, 0, 2)) res = arima_model.fit(dist=False) resid = res.resid plt.plot(resid)
from statsmodels.graphics import tsaplots tsaplots.plot_pacf(resid, lags=25)
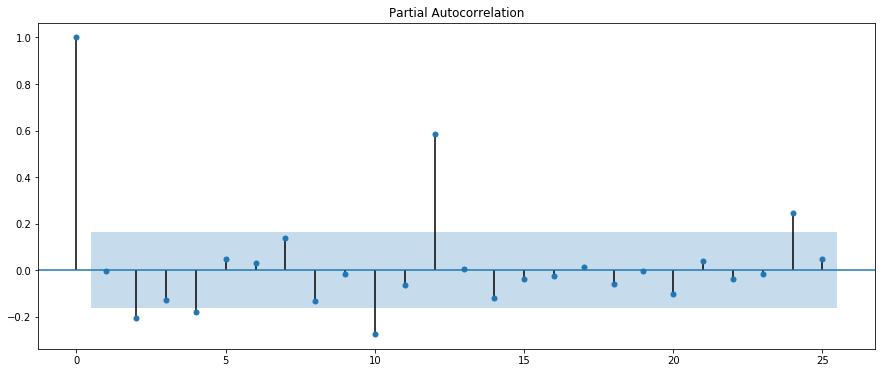
ラグ12, 24みたいな周期的な部分のスパイクが捉えられていないのが分かります。
ARIMAモデルでの時系列予測
一応ARIMAでの予測もやってみましょう。
arima_model = ARIMA(df['Passengers'], order=(4, 0, 2)) res = arima_model.fit(dist=False) arima_predict = res.predict() plt.plot(df['Passengers'], label='observation') plt.plot(arima_predict, '--', label='forcast')
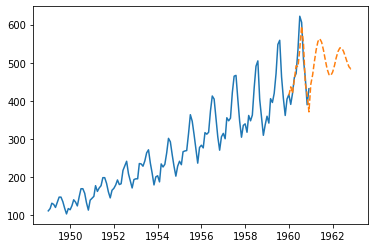
ARIMAモデルは季節成分を考慮しないため、その部分が実測値との差になっている感じがします。次はARIMAモデルに季節変動を加えたSARIMAをモデルを使って予測をしてみたいと思います。
⇒ 【Python】MAモデルによる時系列予測をやってみる
⇒ 【Python】VARモデルによる時系列予測をやってみる
⇒ 【Python】SARIMAモデルによる時系列予測をやってみる



コメント