Contents
はじめに
この記事では、Irisデータセットを用いて構築された決定木モデルの出力結果について、初心者向けに解説します。決定木はデータを分類するためのシンプルな手法であり、その理解はデータサイエンスの基本となります。
Irisデータセットとは
Irisデータセットは、3種類のアヤメ(Setosa、Versicolor、Virginica)の花に関するデータを含んでいます。各花について、がく片と花びらの長さと幅(cm)が測定されています。
決定木モデルの概要
決定木は、与えられたデータを、特徴量に基づいて繰り返し分割することで、データを分類します。このプロセスは、木のような構造を形成し、最終的にはデータをクラスに割り当てる「葉ノード」に到達します。
決定木モデルのトレーニング
まず、scikit-learnの DecisionTreeClassifier を使用して、典型的な分類問題であるIrisデータセットを使って決定木モデルをトレーニングします。
import matplotlib.pyplot as plt from sklearn.tree import DecisionTreeClassifier, plot_tree from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split import pandas as pd # サンプルデータセットのロード(ここではIrisデータセットを使用) data = load_iris() # 説明変数と目的変数をデータフレームにする X = pd.DataFrame(data.data,columns=data.feature_names) y = pd.DataFrame(data.target) # データを訓練セットとテストセットに分割 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 決定木モデルのトレーニング clf = DecisionTreeClassifier(random_state=42) clf.fit(X_train, y_train) # 決定木のプロット plt.figure(figsize=(20,10)) plot_tree(clf, filled=True, feature_names=X.columns, class_names=['setosa', 'versicolor', 'virginica'], rounded=True, proportion=True) plt.show()
<実行結果>
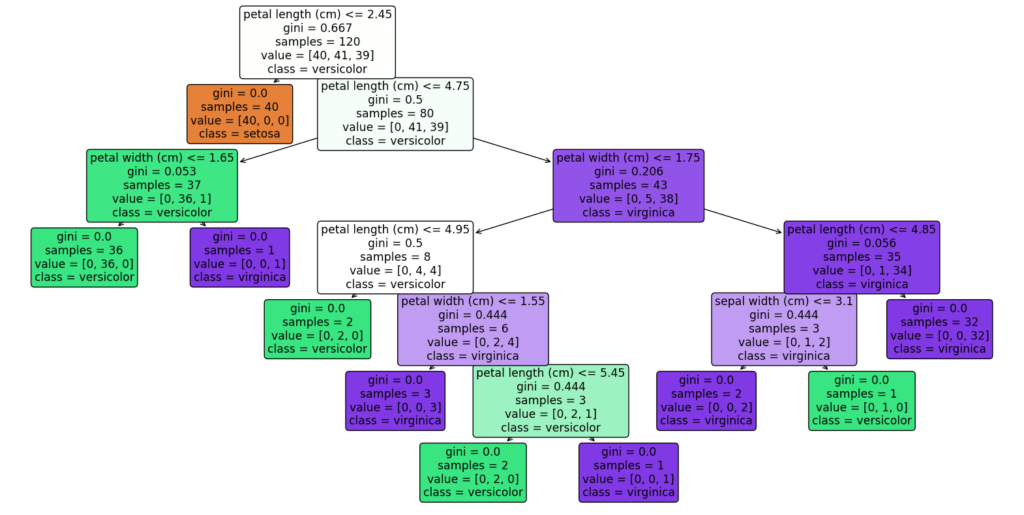
出力結果のノード内の各指標の意味
gini
意味: 「GINI」はジニ不純度(Gini Impurity)を表します。ジニ不純度は、そのノードがどれだけ混合されたクラスから構成されているかを示す指標です。
計算: ジニ不純度は 1 – Σ (p_i)^2(p_i はi番目のクラスに属するサンプルの割合)の式で計算されます。
解釈: ジニ不純度が0の場合、そのノードは完全に純粋(すなわち、1つのクラスのサンプルのみで構成されている)とされます。ジニ不純度が高い(1に近い)場合、そのノードには複数のクラスが均等に混在しています。
samples
意味: 「SAMPLES」はそのノードに到達したサンプルの総数を表します。
解釈: サンプル数は、そのノードのデータ量を示します。サンプル数が多いほどそのノードの分割基準が多くのデータに影響を与えていることを意味します。
class
意味: 「CLASS」はそのノードで最も多いクラス(またはそのノードによって予測されるクラス)を表します。
解釈: 分類タスクにおいて、各ノードは特定のクラスのサンプルを含みます。ノードが葉ノード(最終的な分類が行われるノード)である場合、この「CLASS」はそのノードに属するサンプルの予済クラスとなります。
これらの情報を合わせて考えることで、決定木がどのようにデータを分割し、各クラスを識別しているかの理解が深まります。また、ジニ不純度は分割の効果を、サンプル数はそのノードの影響範囲を、クラスはそのノードの決定結果をそれぞれ示しています。
決定木の第一分岐の解釈
scikit-learnのDecisionTreeClassifier()は引数のmax_depthを指定することで決定木の深さを指定できます、以下は第一分岐だけを確認するコードです
import matplotlib.pyplot as plt from sklearn.tree import DecisionTreeClassifier, plot_tree from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split import pandas as pd # サンプルデータセットのロード(ここではIrisデータセットを使用) data = load_iris() # 説明変数と目的変数をデータフレームにする X = pd.DataFrame(data.data,columns=data.feature_names) y = pd.DataFrame(data.target) # データを訓練セットとテストセットに分割 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 決定木モデルのトレーニング clf = DecisionTreeClassifier(random_state=42,max_depth=1) clf.fit(X_train, y_train) # 決定木のプロット plt.figure(figsize=(20,10)) plot_tree(clf, filled=True, feature_names=X.columns, class_names=['setosa', 'versicolor', 'virginica'], rounded=True) plt.show()
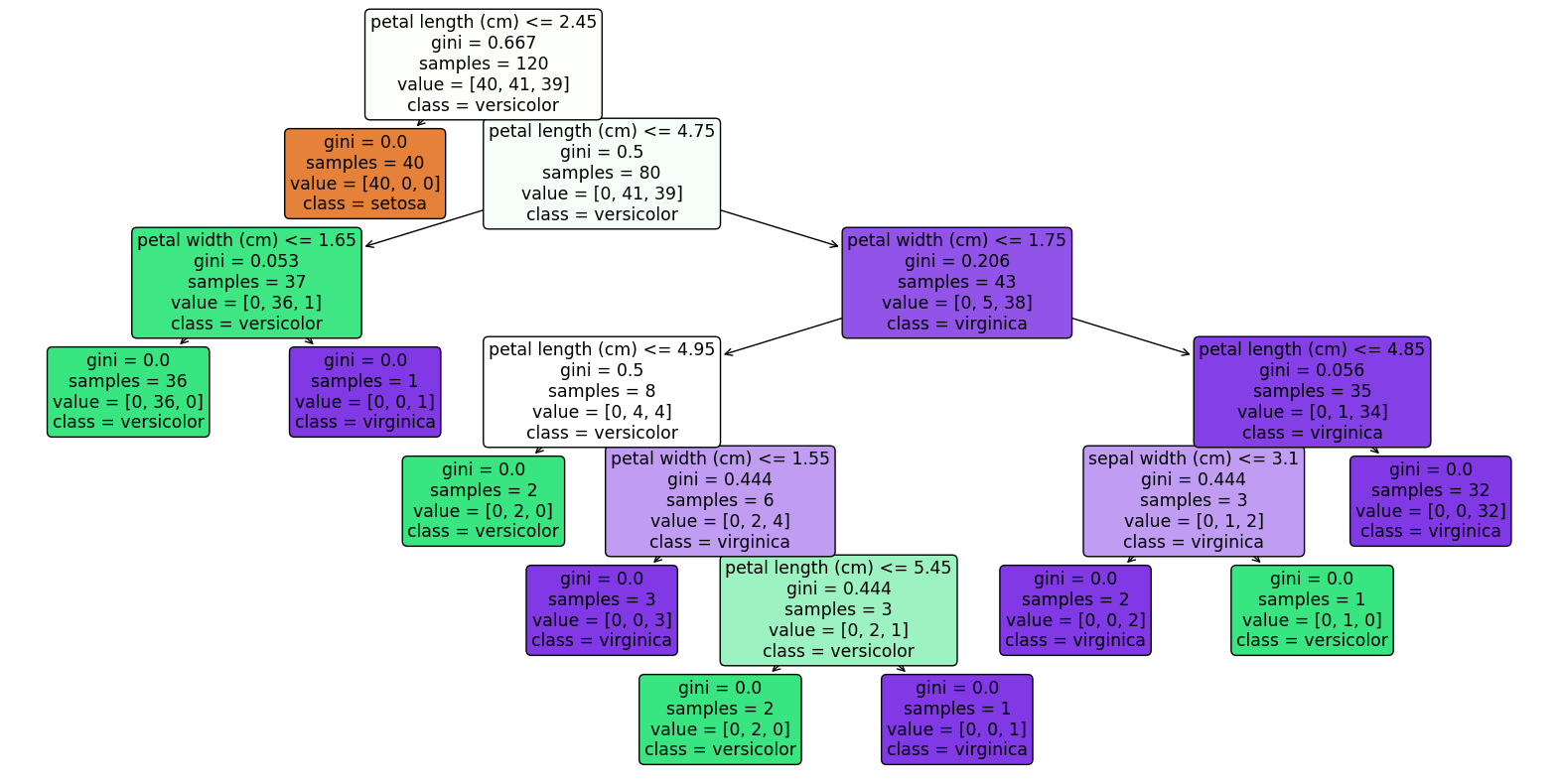
<実行結果>

特徴量と閾値:
第一分岐は petal length (cm) ≤ 2.45 の条件で行われます。
これは、花びらの長さが2.45cm以下かどうかを基準にデータセットを最初に分けることを意味します。
データの分割:
花びらの長さが2.45cm以下のサンプルは、一方の子ノードに分けられます(例: ノード1)。
花びらの長さが2.45cmより大きいサンプルは、別の子ノードに分けられます(例: ノード2)。
クラス別の人数:
第一分岐時点でのクラス別人数は [[40, 41, 39]] です。
これは、ルートノード(ノード0)には、Setosaが40サンプル、Versicolorが41サンプル、Virginicaが39サンプル含まれていることを示しています。これはルートノードでありpetal length (cm) ≤ 2.45 の閾値が適応される前であることに注意してください
葉ノード(ノード①):
クラス別人数: [[40, 0, 0]]
解釈: このノードは、全サンプルのうちアヤメの花びらの長さが2.45cm以下のサンプルが格納されています。クラス別人数は40, 0, 0なので、このノードはSetosaのサンプルのみを含んでいます。つまり、このサンプルデータセットにおいては花びらの長さが2.45cm以下のアヤメはSetosaであると分類されます。
葉ノード(ノード②):
クラス別人数:[[0, 41, 39]]
解釈:このノードは、全サンプルのうちアヤメの花びらの長さが2.45cm以上のサンプルが格納されています
分析の結論
第一分岐における petal length (cm) ≤ 2.45 の条件は、非常に重要な分類基準を提供します。特に、この閾値はIris Setosa(分類0)を他の2種類のアヤメ(VersicolorとVirginica)から効果的に分離するのに役立ちます。実際、花びらの長さが2.45cm以下のサンプルはすべてSetosaに分類されることが、葉ノードのデータ分布から明らかです。
これは、花びらの長さがアヤメの種類を区別するのに特に重要な特徴量であることを示しており、この特徴量はSetosaと他の2種類を区別するのに重要な役割を果たしていることがわかります。このように、第一分岐の閾値分析は、モデルの決定プロセスを理解し、特定の特徴量がどのようにターゲットクラスの識別に寄与するかを解明する上で非常に有用です。ここからさらに分岐を深堀りする場合は第二分岐以降の閾値と説明変数、どれだけ綺麗にクラスが分割されているかジニ係数なども加味して見ていきます
まとめ
今回は、Irisデータセットを用いた決定木分析を実施し、特定のアヤメの種類を識別するための重要な特徴とパターンを特定しました。

分析概要
分析対象: Irisデータセット(Setosa、Versicolor、Virginicaの3種類のアヤメ)
主要な特徴: 花びらとがく片の長さと幅
目的: 各アヤメの種類を効果的に識別するための特徴と閾値を特定
主要な発見
第一分岐ポイント:
花びらの長さが2.45cm以下のアヤメは、一貫してSetosa種と識別されました。これはデータセット内で最も明確な分類基準の一つであり、初期段階の重要な分岐ポイントとなります。
第二分岐以降のポイント:
花びらの長さが2.45cmを超えるアヤメについては、さらなる分析が行われました。その結果Versicolorを識別する条件として花びらの長さが2.45㎝以上4.75㎝未満というルールが明らかになりました。そのほかにも花びらの幅と長さの組み合わせにより、VersicolorとVirginicaが効果的に区分されました。
結論
この分析により、特定の特徴量がアヤメの種類を分類する際にいかに重要かが明らかになりました。特に花びらの長さは初期の分類において極めて重要な指標であることがわかりました。
関連記事:Scikit-learnで作った決定木から閾値とノード数・クラス数などを取得する

コメント