これまで当サイトでもとりあげてきましたが、統計学で出てくる確率的な分布と言われたら、ほとんどの人が、左右対称の釣り鐘型の正規分布を想像すると思います。(【統計学】 正規分布の簡単な説明 を参照)
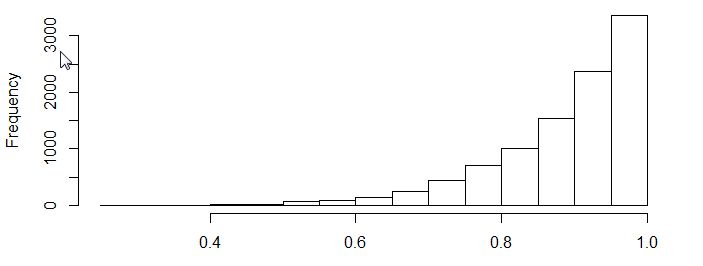
ですが現実では、ある商品の購買状況などの経済現象や、人々の資産状況の分布・株価の変動率などでは、皆さんおなじみの左右対称の釣り鐘型の正規分布ではなく

こういう極端な分布になることが、しばしばあります。統計分析では、よく中心極限定理から正規分布と仮定して検定・推定を行いますが、上の図のような分布は、到底正規分布にはなりそうにもないですね・・・。
こんな分布のものを、正規分布を仮定した多変量解析なんかしても有用な結果が得られるはずもありません。これこそが今日紹介する、「べき分布」です。
ベキ分布は1890年代にイタリアのパレートが、収入の分布を分析した時に発見したものです。その時は正規分布が主流であまり注目されていなかったらしいのですが、1950年代に、アメリカのグーテンベルクとリヒターが地震の大きさと頻度を研究していたときに、これらがベキ乗則に従っていることを発見したことをきっかけに、
近年では株価、為替などの市場価格の変動、所得の分布といった経済現象は正規分布ではなく、べき分布に従っているとして研究が進みつつあります。
金融工学で用いられる※ブラック=ショールズモデルは、正規分布を前提としたモデルなのですが、現実の分布はべき分布だから、ブラック=ショールズ式は現実には全く当てはまらないという意見もあるようです。
※ブラックショールズモデル:オプション商品の価格の現在割引価値を求める計算式のこと。発見者のブラック=ショールズはこの式でノーベル経済学賞を受賞しています。
ベキ分布の特徴としては、平均や分散という概念がないという点です。そして、分布が左右対称になる正規分布とは、ほぼ対照的に、中央値・最頻値が分布のぼぼ端に出てきます。
そこから大きな値から長くなだらかな曲線を作りながら長い裾野(ロングテール)を作っていきます。他にも、べき分布はどの尺度で拡大したり縮小してみても、常に同じような分布になるという「スケールの不変性」という特性があります。
ベキ分布は正規分布や二項分布のような数ある確率分布の一つに過ぎませんが、地震やバブルの崩壊といった正規分布では、通常起こりえない程度の確率の事象が起こってしまう確率を考える上で、有効な分布であると考えられており、地震やバブルの予測というのは今研究がさかんな分野で、べき分布はこれからさらに重要性が高まっていくと思われます。
ですが、べき分布にはいろいろと問題があるのです・・・


コメント