二項分布を使ってソシャゲガチャでSSRの出現確率を計算する
今回は統計学の基本である『ベルヌーイ試行』と『二項分布』について解説しつつPythonというプログラミング言語を使ったシュミレーションを行っていきたいと思います。
今ここにSSRである高垣楓(夜中の誘い)が当たるガチャがあるとします。 ネットの情報からSSRの高垣楓が当たる確率は1%だとの情報を運良くゲットしたとしましょう。


あなたはこのSSRの高垣楓がとても欲しくて、バイトで稼いだ大事な生活費と交遊費のほとんどを今回のデレステのSSRガチャにつぎ込もうと考えています。
そんなときあなたは「何万円用意すれば、このSSR高垣楓(夜中の誘い)を確実に引くことができるでしょうか?」と考えたとします。今日はこの確率を統計学を使って計算していきたいと思います。
統計学の世界では、「ガチャを回す→結果は当たりorはずれ」のような試行結果が2パターンになる事象を『ベルヌーイ試行』と言います。ちなみにこのベルヌーイ試行が成立すっる前提条件としては各試行が『独立』していることがあります。
各事象が『独立』しているということはつまり、今回の例だとn回目のガチャの回した結果によってn+1回目のガチャでSSR高垣楓が出る確率は変化はないということを言意味しています。
そして、SSRの高垣楓が当たる確率をp, 外れる確率を(1−p)であるガチャをn回引くとすると、デレステのガチャを回してSSR高垣楓が出てくる確率は、試行回数nと当たる確率pで表現される二項分布に従います。二項分布のパラメータは試行回数nと目的の象の起こる確率pなのでBi(n,p)と書いたりします。
今回はSSRの出現率は0.5%とするので、p=0.005となります。試行回数はとりあえず200回としましょう。
二項分布の計算式は
f(x)=nCxpx(1−p)n−x
それでは最初に書いたデレステのSSRガチャの例を、二項分布でみてみましょう。 SSRの高垣楓が当たる確率は0.5%、引く回数は100回引くとすると、Bi(100,0.005)なので、このときの確率分布は、
f(x)=100C1x0.005x(1−0.005)100−x
Pythonで二項分布の確率計算をしてみる
というわけでこの確率をPythonというプログラミング言語で計算してみましょう。Pythonはこういった確率計算やデータ分析に非常に便利かつ書きやすいので、プログラミング初心者の方にもおすすめです。
Pythonで二項分布を計算する際は、Numpyのnp.random.binomial()が使うと便利です。今回は計算結果をグラフでプロットするところまで行きたいと思います。
import matplotlib.pyplot as plt
from pylab import rcParams
import matplotlib as mpl
plt.xkcd()
font = {"family":"Noto Sans CJK JP"}
mpl.rc('font', **font)
# 100回ガチャを回してSSRはどのぐらい出るのか?という試行を1000回行う
size=1000
n=100
gatya = np.random.binomial(n=100, p=0.005, size=size)
p_0=(1-list(gatya).count(0)/size)*100
print(str(n)+'回ガチャを回してSSRが最低一回は出る確率は'+str(p_0)+'%')
xlabel=(str(n)+'回ガチャを回してSSRが出る回数')
ylabel=(str(size)+'回繰り返して起こった事象の出現回数')
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.hist(gatya,bins=24)
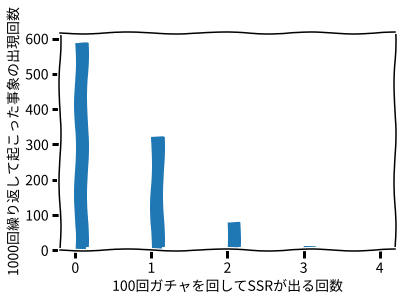
100回ガチャを回してSSRが最低1回は出る確率は41.300000000000004%で最低一回は出る確率は試行回数を上げていくとドンドン大きくなっていきます。900回くらいまで引き上げると99%の確率で最低1回はSSRが引けるという計算になりました。
Matplotlibで日本語入力しようとすると文字化けしてしまう人は以下の記事を参照して日本語化していただけると幸いです。
終わり
統計学や確率というものは一見小難しくて敬遠してしまいがちですが、現実の例に当てはめてみると考えるのが楽しくなると思います。特にベルヌーイ事象と二項分布は現実でも結構使えるので、知っておくと簡単な確率は計算できるようになります。




コメント