素数とは何か
素数とは素因数分解した際に1とその数でしか割れない数のことをさす。

Pythonで素因数分解をやってみる
import sympy as sym
sym.factorint(113)
#実行結果
{113: 1}
import sympy as sym
sym.factorint(200)
#<実行結果>
{2: 3, 5: 2}
素数は暗号の元
現在の暗号の基本は素数同士の掛け算にあります。例えば素数である113×41は4633と簡単に計算することができますが、4633を113×41と推測するのは素数を総当たりするしかないため、非常に手間がかかります。
もちろん実際の暗号に使われている素数は100桁×100桁など非常に大きく高性能になった現代のコンピューターですら途方もない時間が掛かります。
暗号の基本的な仕組みはコレでコンピューターで頑張れば理論上解けないことはないけど、計算するのに数百年近くため、実質的に解読不可能という感じです。
インターネットの通信においてこの素数を性質を利用しているのが、「RSA暗号」です。RSA暗号では「暗号化するためのカギ(公開鍵)」と「暗号を解くためのカギ(秘密鍵)」の2つのカギをペアで使用する暗号化方式です。
RSA暗号における暗号化のためのカギは素数同士を掛け合わせた値になります。そして、その公開鍵の値のもとになった2つの素数が秘密鍵になります。
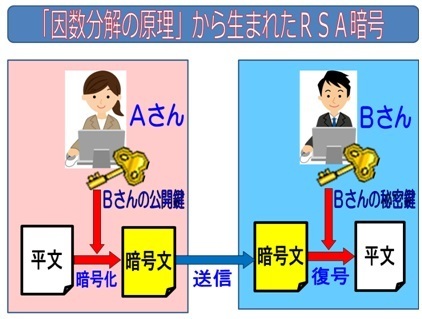
引用:http://electronic-journal.seesaa.net/article/455358651.html
通信の大まかな流れとしては、まず公開鍵を公開して自分あてのメッセージは公開鍵を使用して暗号化して相手に送ります。そして、受け取った側は公開鍵のもとになった2つの素数である秘密鍵を使って暗号化されたデータを解読します。
これならばもし途中で悪意のある第3者に中身を見られても暗号化されており、しかも暗号は秘密鍵がないと事実上解読できないので、情報が洩れる心配はありません。この公開鍵と秘密鍵を使った暗号化の仕組みはインターネット上で『電子署名』という形で使用されています。




コメント