こんにちは、ミナピピン(@python_mllover)です。この前の記事でP値について解説したので、今回はは実際にPythonでscipyというライブラリを使って、仮説検定を行いP値を計算し結果の解釈したいと思います。
Contents
使用するデータと分析テーマ
データは機械学習でアヤメのデータです。Anacondaに付属のScikit-learnを使用します。
関連記事:【Python】Anacondaのインストールと初期設定から便利な使い方までを徹底解説!
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
from sklearn.datasets import load_iris
%matplotlib inline
data = pd.DataFrame(load_iris().data, columns=load_iris().feature_names)
target = load_iris().target
target_list = []
for i in range(len(target)):
num = target[i]
if num == 0:
num = load_iris().target_names[0]
elif num == 1:
num = load_iris().target_names[1]
elif num == 2:
num = load_iris().target_names[2]
target_list.append(num)
target = pd.DataFrame(target_list, columns=['species'])
df = pd.concat([data, target], axis=1)
df
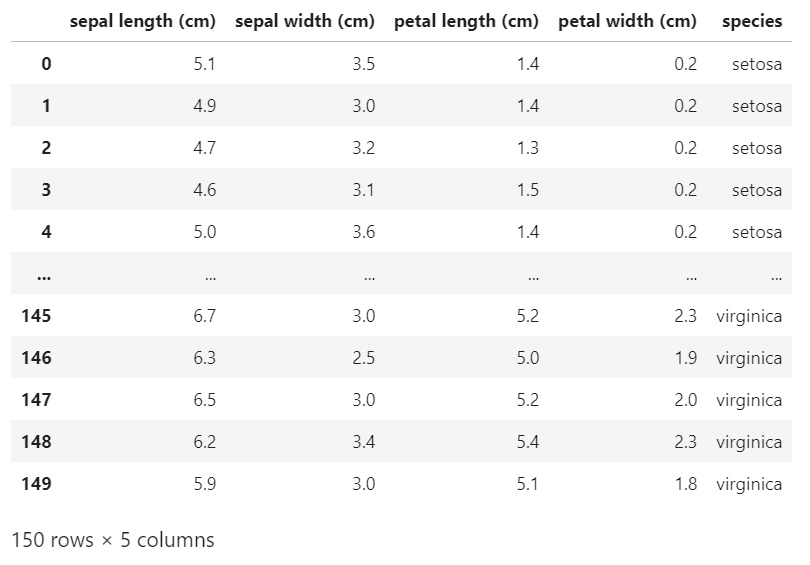
データができたら次は基本統計量を確認しましょう。
# データの基本統計量を確認する df.describe()

次にGroup BYを使ってアヤメの種類別の統計量を集計します。
# アヤメの種類別に基本統計量を集計する
df.groupby('species').describe()
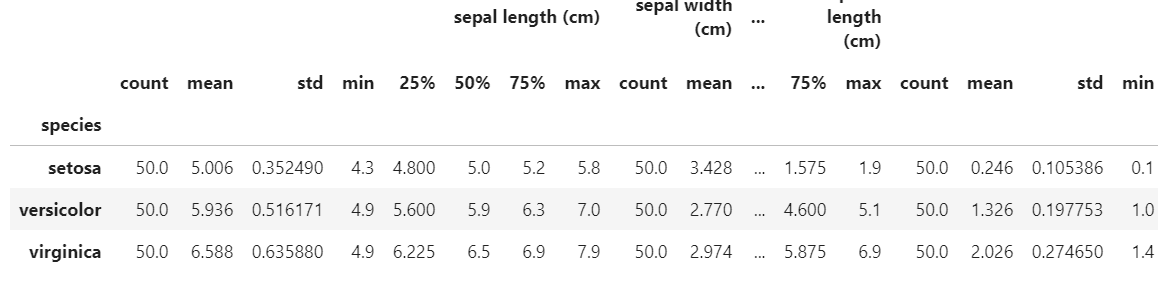
データの性質はざっくり確認できたので、このデータをもとに仮説を立ててそれを統計的に検定したいと思います。とりあえず今回のテーマは「setosaとvirginicaのがく片の長さ(sepal length(㎝))の平均には差がある」という仮説を立てて2標本の標本平均の差の検定を行いたいと思います。
仮説検定のプロセス
最初に仮説検定のプロセスを確認します。
①帰無仮説と対立仮説、検定の手法を確認
まず仮説の立て方ですが、基本的には証明したい方を対立仮説にして、帰無仮説に否定したい説を設定します。今回の場合であれば、「setosaとvirginicaがく片の長さ(sepal_width)の平均には差がない」を帰無仮説として、「setosaとvirginicaがく片の長さ(sepal_width)の平均には差がある」を対立仮説とします。
2.有意水準を決める
帰無仮説を棄却するに足るための水準を決めます。有意水準は検定の条件によって変わりますが、基本的には5%、つまりP<=0.05であれば帰無仮説を棄却すると設定することが多いです。棄却域は第一種の過誤、つまり間違っているものを正解としてしまう確率なので、医療のワクチンなどミスが許されないものは棄却域を5%ではなく1%などにするケースがあります。
3.検定の方法を決める
仮説検定には、片側検定、両側検定とがあります。同一の有意水準を使った場合でも、どちらの検定を用いるかで、棄却域が変わってきます。(片側ならp<=0.05、両側ならp<=0.025)
片側検定か両側検定かは、問題によって決まります。どちらの検定が自然であるかによって決まるものであり、厳密な基準があるわけではありません。
また今回は母集団全てのデータ、つまり全てsetosaとvirginicaのがく片の長さを集計したわけではないので、標本同士の検定という事になります。この場合はz検定ではなくt検定で検定を行います。基本的に母平均や母分散が取得できるケースは稀なので現実の仮説検定はt検定で行うことが多いです。
Pythonにt検定を実装する
それではPythonでt検定を実装してみましょう。今回のような「2つの集団からの各対象から、1つずつ値を抜き出してきて、平均値の差が有意かどうかを調べる検定」を行いたい場合はttest_ind()という関数を使用します。
# t検定を実装する t, p = stats.ttest_ind(setosa['sepal length (cm)'], virginica['sepal length (cm)'], equal_var=False) print( "p値 = ", p)
<実行結果>
p値 = 3.9668672709859296e-25
P値が0.05より小さいので、帰無仮説を棄却し、対立仮説=「setosaとvirginicaがく片の長さ(sepal_width)の平均には差がある」を採用することができます。
t検定の2つの前提条件
これでt検定自体はできましたが、t検定は使用するデータに対して2つの重要な制約があります。
1つ目は、データが正規分布にしたがっているかどうか
2つ目は、両標本の分散が等しいかどうか
①正規性の検定
1つ目のデータが正規分にしたがっているかどうかは、QQプロットなどで可視化する方法もありますが、量的にはシャピロ・ウィクス検定で確かめることができます。(帰無仮説:本データは正規分布に従う、対立仮説:本データは正規分布に従わない)
⇒ 【Python】正規性検定(シャピロ・ウィクス検定/QQプロット)を実装する
②標本の分散の検定
両標本の分散が等しいかどうかは、等分散性の検定(F検定)という方法で確かめることができる。(帰無仮説:両標本の分散は等しい、対立仮説:両標本の分散は異なる)
⇒ 【Python】F検定を実装する
基本的にはt検定を使う前にデータがこの2つの条件を満たしているかを確認する必要あるということを覚えておきましょう。
終わり
Pythonでの統計的な計算は関数を数行書くだけで終わりますが、コードの意味や結果の解釈の部分をちゃんと理解するという部分が本題になります。実務で携わっていて思うのはPythonが書けるから年収が高いのではなく統計の知識があり、それをPythonで適切に実装できる人は重宝され年収は高くなる傾向にあるってことですね。Pythonが書けるだけでは年収は上がりません。



コメント