【Python】statsmodelsで時系列データの基本的な前処理をやってみる

こんにちは、ミナピピン(@python_mllover)です。Pythonのライブラリである「statsmodels」を用いて時系列データでの基本的な前処理を実装していきます。

Contents

statsmodelsとは
基礎分析の流れ
使用するデータ
Pythonで読み込みデータを可視化する
時系列データの概念
過去の値の現在のデータに対する影響度を確認する
- 自己相関
時系列モデルにおける確率過程

定常性を持たせるためにデータを加工する
- ADF検定で定常性をチェックする
- 終わり

statsmodelsとは

統計モデルの実装のために必要なものがたくさん揃っている便利すぎるライブラリです。scikit-learnみたいな感じですが、scikit-learnの方が機械学習寄りでstatsmodelsの方が統計寄りという印象です。

基礎分析の流れ

使用するデータを確認、時系列分析の基本説明
基本統計量の確認
データを定常な状態にする
定常性の確認

使用するデータ

今回使用するのは、航空会社の乗客数データです

Air Passengers

Number of air passengers per month

csv落としてディレクトリに配置したりするのがめんどくさいという場合は、有志が作成したライブラリから読み込むこともできます。

# ライブラリをインストールする
$ pip install pydse

Pythonで読み込みデータを可視化する

# ライブラリの読み込み
import numpy as np
from pydse import data
%matplotlib inline

df = data.airline_passengers()
df.plot()

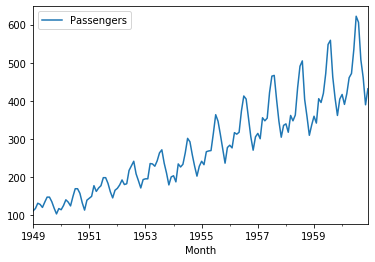
申し訳ないくらい特徴がわかりやすいデータですね。これでデータの準備はできました。

時系列データの概念

このような何も加工していないデータは傾向変動(トレンド)、季節変動、不規則変動の3つに分解することができます。

傾向変動(トレンド)：

時間とともに平均値が増加/減少する成分

季節変動：

季節によって左右される成分

不規則変動：

説明がつかない部分、イレギュラーやノイズと呼ばれる

過去の値の現在のデータに対する影響度を確認する

時系列分析で大事な考え方として、定常・単位根過程の他に「過去の値の現在のデータに対する影響しているか」というものがあります。これを確認する指標が「自己相関」「偏自己相関」になります。

普通の分析だとXとYという別々の変数の相関度を回帰分析なんかで見ますが、時系列分析で過去のデータとの相関具合を確認します。

自己相関

時系列上にある異なる点同士の相関のことを自己相関と言います。時系列分析がただの回帰分析と大きく違うのがデータの前後の関係を考慮する点です。自己相関を用いることで、データの前後の関係を表現します。自己相関はコレログラムというグラフで表すことができます。statsmodelsではgraphicsのplot_acfでコレログラムを描画することができます。また、今回は割愛しますが、自己相関と似ているもので、「偏自己相関」というものがあります。偏自己相関はplot_pacfで描画することができます。今回のデータの自己相関を図で表すとこのようになります。

import statsmodels.api as sm

# グラフを横長にする
from matplotlib.pylab import rcParams 
rcParams['figure.figsize'] = 15, 6 
# 自己相関のグラフ 
fig = plt.figure(figsize=(12,8)) 
ax1 = fig.add_subplot(211) 
fig = sm.graphics.tsa.plot_acf(df['diff_change'][1:], lags=70, ax=ax1) 
ax2 = fig.add_subplot(212) 
fig = sm.graphics.tsa.plot_pacf(df['diff_change'][1:], lags=70, ax=ax2)

<実行結果>

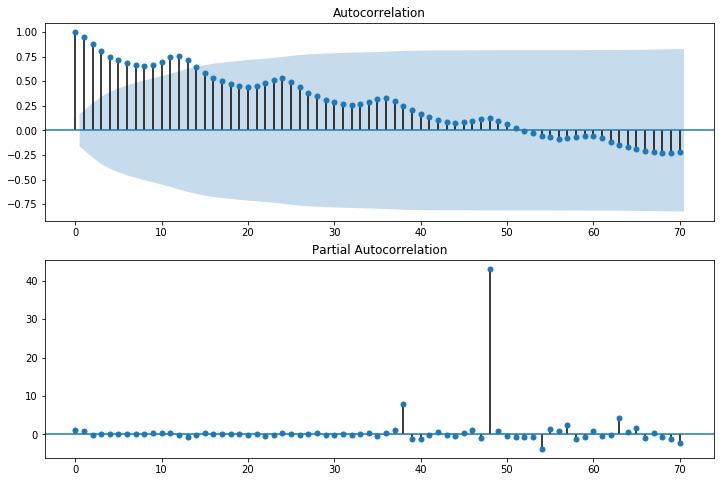
「AutoCorrelation」がコレログラムです。ちなみに水色になっている部分は95％信頼区間を表しています。この信頼区間外にデータが及んでいる点は統計的に有意差があると言えます。横軸が48の時に大きくなっており、48ヶ月前のデータと特に似ているということがわかります。つまり48ヶ月(約4年)ごとの周期性があるということになります。

<自己相関係数>
自己相関係数の横軸、ラグ0は常に1.0（ラグ0はデータをズラさないから）。
ラグ数が増えると自己相関係数の値が小さくなってるので、自己相関がありそう
※自己相関が無いときは、ラグ0を除き、自己相関係数の値が95%信頼区間にほぼ全部のデータが入る。（この時は過去の影響から良さげな予測モデルは作れない）

<偏自己相関>
95%の信頼区間を超えた有意差のある意味のある差、グラフで周辺と比べて突出したところを「スパイク」と言います。

statsmodelsのseasonal_decomposeを使うと、サクッと時系列データをトレンド成分と周期成分と残差に分解することができ、しかもそのままプロットできます。

時系列モデルにおける確率過程

時系列データを予測するために、簡単な確率モデルを考えます。モデルを考える上では、確率過程を使います。その中でもっとも重要なのが「定常確率過程」です。

時系列データ分析でまず重要なのは「そのデータが(弱)定常性」を持っているかどうかです。時系列分析でよく使われる時系列モデルはデータが定常であることが前提なのでデータが定常でないとモデルを使用することができません。

⇒ 【時系列分析】定常性とは何かを分かりやすく説明する

定常性を持たせるためにデータを加工する

ですが、上述したように時系列データはトレンドや季節変動の成分が含まれているので、基本的に生データで定常性を持っていることはまずありえません。なので時系列分析では、データを加工して定常性を持っているような形に変換するという処理が必要になります。その方法として、「季節調整」「移動平均」「差分」「対数変換」などがあります。差分や対数化はPythonで以下に実装できます。

# 差分を計算する
df['diff'] = df['Passengers'].diff()

# 変化率を計算する
df['diff_change'] = df['Passengers'].pct_change()

#対数変換
df['Pass_log'] = np.log(df['Passengers']) 

# 対数差分
df['diff_log'] = df['Pass_log'].diff()

株価データなど正の方に大きく上昇しているデータに対しては対数変換して、差分や変化率を計算するケースが多いです。(他にも移動平均や指数移動平均や中心化移動平均をとることもあります)対数差分をとるとこんな感じになります。

さっきの斜め上にジグザグしていた形から一定の周期で上下に変動する定常的な動きに変換できていることが分かります。

このように原系列が非定常であり、その差分系列が定常であるような時系列を単位根過程または1次和分過程といいます。またこれを一般化し、 d−1 階差分が非定常で、 d 階差分が定常であるような時系列を d 次和分過程といいます。つまり、時系列が和分過程であれば、差分変換によって定常にすることができます。

⇒　単位根過程とはなにか

ADF検定で定常性をチェックする

定常性の確認はアドバンスド・ディッキー・フラー検定[ADF検定]で調べます。ADF検定はディッキー・フラー検定[DF検定]の拡張版で定常性をチェックするための統計的検定の1つです。DF検定よりもやや定常性の判定が緩いのが特徴です。

そしてADF検定での帰無仮説は、「データは非定常である」いうことで、検定結果は検定統計量と信頼度の差の臨界値で構成されており、「検定統計量」が「臨界値」よりも小さければ、帰無仮説を棄却し、その時系列データが定常であると言えます。ADF検定はPythonでは以下のように実装できます

# ライブラリを読み込む
from statsmodels.tsa.stattools import adfuller
import matplotlib.pyplot as plt
import pandas as pd 
# ADF検定
print('Results of Dickey-Fuller Examination:')
# dftest = adfuller(df['diff_change'][1:], autolag='AIC')
dftest = adfuller(df['diff_change'][1:])
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
   dfoutput['Critical Value (%s)'%key] = value
print(dfoutput)

<実行結果>

Results of Dickey-Fuller Examination:
Test Statistic                  -2.926109
p-value                          0.042395
#Lags Used                      14.000000
Number of Observations Used    128.000000
Critical Value (1%)             -3.482501
Critical Value (5%)             -2.884398
Critical Value (10%)            -2.578960
dtype: float64

実行結果の出力はTest StatisticとCritical Valueを見比べて結果を確認します。Test Statisticの値が、Critical Value(5％)を下回っているので定常とみなすことができます。これによってARモデルなどの定常過程の時系列モデルを適用することが可能になります。

⇒ 【Python】ARモデルで時系列データ分析をやってみる

1. データが値の間に依存性の無い定常なケース。
残差をホワイトノイズとしてモデル化することができる簡単なケースですが、こんなことは非常にまれらしいです。

2. データが値の間に依存性があるケース。
この場合、データを予測するためにARIMAのような統計モデルを使用する必要があります。