Contents
ニューラルネットワークとは何か?

ニューラルネットワークは機械学習(マシンラーニング)におけるモデリング手法の1つで、人間の脳の仕組みを模倣したモデルです。とは言ってもニューラルネットワークは脳の何十億というニューロンを正確にモデル化しようとしているものではありません。単にそれを単純化し動作可能なものにしようとしているのです。
ニューラルネットワークではデータ(数値)を入力すると、その数値を次の層に重みをかけて伝播されます。これは、人間の脳においてシナプスが重みをかけて接続され、そして、ニューロンがアウトプットを生成し、そのアウトプットが次のレベルに接続されるという一連のプロセスに類似しています。
具体的に私たちが日常生活で何かを感じたり触ったりしたとき、脳にその情報が入力され、そのプロセスがネットワーク内でモデル化されます。まだ人間の脳を完全に再現することはできませんが、ニューラルネットワークは人間の脳の仕組みを簡単に模したものであり、それによって将来的にはコンピューターにも人間と同じようなこと、つまりモノ・人の認識や会話などができるようになる可能性があります。
ニューラルネットワークとディープラーニング
人間の脳はニューロン(neuron)という神経細胞1つ1つで構成され、それらが相互に繋がっているネットワーク構造になっています。そして脳細胞(ニューロン)から別のニューロンにシグナルを伝達する伝線のことを「シナプス」と言います。つまりニューロンはシナプスから電気や化学反応のシグナルを発信して情報をやり取りしています。
そして、ニューラルネットワークは、こうした人間の脳の仕組みを単純に模倣した構造となっており、これが現在の人工知能の元です。正確には現在の人工知能と呼ばれているもののアルゴリズムはニューラルネットワークの中間層を何千何万層にも増やしたモデルであり、そういったものを「深層学習(ディープラーニング)」と呼んでいるだけです。
ニューラルネットワークを理解する上において抑えておきたい単語は、「ニューロン」「(多層)パーセプトロン」「活性関数」「シグモイド関数」というやつらです。こいつらの意味がわかれば、ニューラルネットワークが何をしているアルゴリズムなのかはかざっくりと理解できると思います。
ニューロンと発火
ニューラルネットワークにおいて人間の脳細胞を模した「ニューロン」(↓の図だと〇のやつ)は、基本的に0で入力値(X₁,₂,₃)に重み(W₁,₂,₃)を掛けた数値が入ることによって上昇していき、これがあるしきい値を超えると”1″,になります。このニューロンが1を超えることを「発火」と言います。これを超えなければ”0″となります。
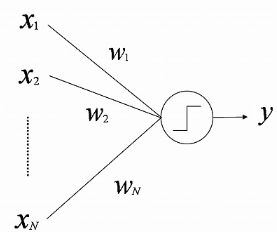
http://ifs.nog.cc/fishwin.hp.infoseek.co.jp/hp/etc/soft_computing/mlp.htmlより引用
まあ実際に分析で使う際は入力値xのところにバイアスbを加えるのが一般的にです。
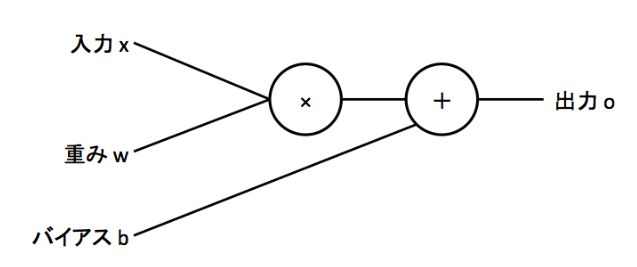
https://qiita.com/perrying/items/6b782a21e0b105ea875cより引用
基本的にコンピューターは情報を1と0の2進法で表現しますし、物事の判断も1か0で判断します。この1と0の概念はニューラルネットワークだけではなく機械学習やひいては他のプログラミングでも使う概念ですので、覚えておきましょう。
パーセプトロンとは何か?
ニューラルネットワークについて勉強すると絶対出てくる単語の1つに「パーセプトロン」というのがあります。「パーセプトロン」とは簡単に言うとニューラルネットワークの一種であり、正式にはパーセプトロンアルゴリズムと言います。
ディープラーニングを勉強する上においてなぜ「パーセプトロン」を学ぶ必要があるのかというと、パーセプトロンはディープラーニングの元になるアルゴリズムだからです。
基本的にパーセプトロンもニューラルネットワークもディープラーニングもやっていることは同じです。ただやっていることの複雑さで定義が変わります。これらの明確な線引きは人によって違うので、これくらいの認識でいいと思います。
モデルの難易度的には、単純パーセプトロン→多層パーセプトロン(ニューラルネットワーク)→ディープラーニングという感じになっています。
なので、まず基本のパーセプトロンを理解しないとディープラーニングについて何も理解できません。そのため、どのディープラーニング系の参考書を開いてもまず最初の説明にパーセプトロンが登場します。そして、パーセプトロン(ディープラーニング)は「分類」と「回帰」の2パターンがあるということを抑えておいてください。今のところ「分類」の方が精度が良いのでよく使われています。
パーセプトロンの仕組み
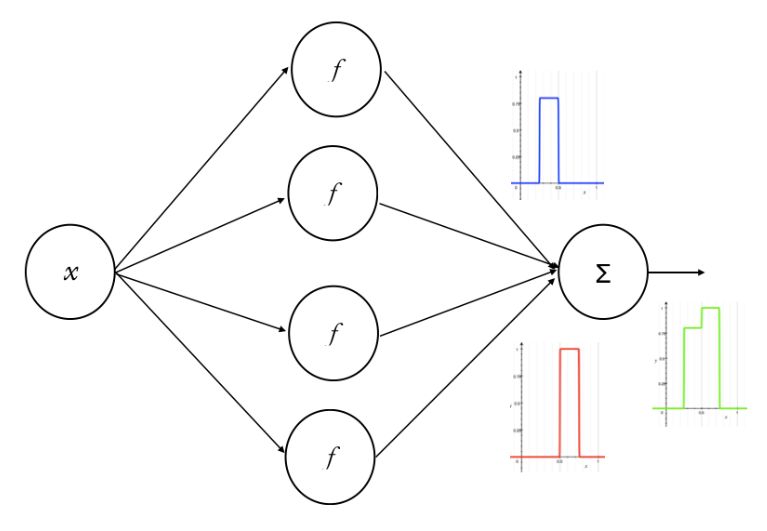
https://qiita.com/perrying/items/6b782a21e0b105ea875c
パーセプトロンは、上述したように人間の脳を簡単に模したネットワークであり、そのネットワークは↑の図のように、大きく「入力層」と「中間層」と「出力層」の3つの部分に分けて構成されています。
3つの各層の数は特に決まっているわけではなくデータによって決まります。例えばよくあるPython「Keras」というライブラリを使った数字認識なんかであれば入力層のデータは教師データ1つ1つに格納されているデータの数であり、画像の色を数値の行列に直した16×16=256の数値で構成されたデータなので256になります。次の中間層は任意で設定するもので多ければ多いほど複雑なモデルが作れるので、データに柔軟に対応することができます。ただ多くすればするほど計算量が膨大になります。
そして、最後の出力層は答えの数です。例えば0~9の数字を認識を学習させる場合ならば、答えの数である出力層は0,1,2,3,4,5,6,7,8,9の10個になります。他にも株価データの場合ならば上がるか・下がるかの2つなので0,1の2つになります。回帰ならば出力層は1つです。
「入力層」では、外部からデータを入力します。そして、次の「中間層」では入力層からのデータに「重み」を掛けるという計算処理を行い、そこに活性化関数を掛けます。この活性化関数には「シグモイド関数」や「RELU関数」が使われることが一般的です。最後の「出力層」では、中間層から来た数値を「恒等関数(回帰の場合)」または「ソフトマックス関数(分類の場合)」にかけた数値を出力します。
そして、ここからが肝心なのですが、一般的な教師あり学習の場合、他の機械学習アルゴリズムと同じように、出力と正解の値の「誤差(損失)」を計算し、それが最小になるようにシナプスの数値にあたる「重み」を更新します。「重み」の更新量は予め設定した学習率×誤差で計算することができます。
パーセプトロンには「単純パーセプトロン」と「多層パーセプトロン」の2つがあります。単純パーセプトロンとはネットワークが入力層と出力層のみの2層からなるもので1960年代に考案されたものですが、これでは非線形のモデルを計算することができないという問題点がありました。そこで考案されたのが多層パーセプトロンであり、世間一般でいうニューラルネットワーク・というのは多層パーセプトロンのことを指します。
ニューラルネットワーク(多層パーセプトロン)
多層パーセプトロンは単純パーセプトロンに中間層をさらに増やすことで単純パーセプトロンよりもより複雑な表現をすることが可能にしたものです。
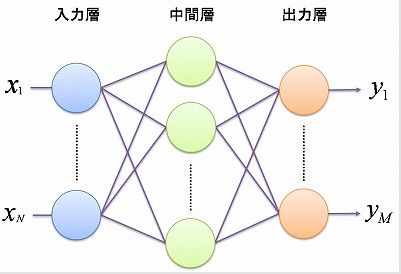
http://ifs.nog.cc/fishwin.hp.infoseek.co.jp/hp/etc/soft_computing/mlp.htmlより引用
多層パーセプトロンの大きな特徴としては、特徴量の決定が容易だという点があります。特徴量とは何かというとモデルにおける変数xのことです。というのも例えば線形回帰モデルならy=ax+bで非線形回帰モデルならy=ax²+bという風にデータの性質でaとbの値は変わりますが、特徴量は変わりません。
ですが、多層パーセプトロンであればデータの真の形が線形であろうと非線形であろうと柔軟に適応させることでき、そのうえで最適なほうを選択することできます。
活性化関数とは?
上でもチラッと触れましたが、ニューラルネットワークや機械学習でよく出てくるワードの1つに活性化関数というものがあります。この「活性化関数」とは簡単に言うと、入力の総和を出力に変換する関数です。
ニューラルネットワークにおいては各ニューロンから受け取ったデータに重みをかけた数値を次の層に伝播させるわけですが、その次の層に流すまえに各ニューロンの数値にこの活性化関数を通します。上述したように、活性化関数に使われる関数には「シグモイド関数」や「ステップ関数」「RELU関数」などがありますが、0か1かではなく0~1の間のどの値でも取ることのできるシグモイド関数を使うのが一般的です。
つまり、各ニューロンから次のニューロンに伝播される数値は0~1であり、1より小さい数が伝播されそれにさらにシグモイド関数を掛け合わせるので、伝播されるにしたがってその値は限りなく小さくなっていきます(0.1×0.1×0.1・・・)。
なので、中間層が何層も存在するディープラーニングでシグモイド関数を使うと、伝播する値が限りなく0になってしまい伝達がまともにできなくなってしまう=つまり何も伝わらなくなる「勾配消失」という問題が発生します。
まあこれは他の関数を使うなどで解決することが可能で、近年はRelu関数などのより有効な活性化関数が誕生したので、特に問題でなくなっています。そして、ここまでの入力層→中間層→出力層までの計算を「順伝播」と言います。
ここから出力されたデータと正解のデータの誤差を計算し、それが最小になる重みを見つけるという作業をします。これは出力層での誤差を受けて、それが最小になるように入力層部分の重みを変更するという、さっきとは逆の流れなので「逆伝播」と言われます。
逆伝播~誤差と重みの計算
機械学習の大まかな手順は「モデルの作成」→「計算した値と正解のデータの誤差を計算する」→「その誤差が最小になるパラメーターを見つける」という流れです。
この誤差の計算ですが、単に「出力された値ー正解の値」ではなく、いろいろ加工する必要があります。そのデータの加工方法は、回帰であれば誤差(出力された値ー正解の値)を2乗する「誤差2乗法」、分類であれば「交差エントロピー」を使うのが一般的です。
そして、それによって計算された誤差と重みによる関数を「誤差関数」と言います。つまりニューラルネットワークとは「重みを更新する」→「ネットワークを再計算し誤差を計算する」→「それの繰り返しによってできた誤差関数が最小となる値を見つける」という作業になります。
これが結構計算量がかかる作業で、実際にプログラムで再現しても時間が掛かります。そして誤差と重みの関係を表した関数は曲線であり、計算としてはこの曲線の底を探しながら下に下に降りていくため、「勾配降下法」と言われています。
この学習の方法にはデータを複数に分割して複数回計算するミニバッチ学習というのが一般的です。(ミニバッチ学習においては確率的勾配降下法と言います。)
というのも、ミニバッチ学習をせず与えられたデータをすべて一度に計算するとそのデータにだけ異様に当てはまりが良くなってしまう局所最適解(過学習)が起こる可能性があるためです。
終わり~ディープラーニングの現実と勉強方法
以上が「ニューラルネットワーク」と「ディープラーニング」についての簡単な説明です。この一連の流れをpythonの機械学習ライブラリを使って計算するわけですが、TensorflowやKerasとかで計算する場合は関数を入力すればPCが勝手に計算してくれます。
「ニューラルネットワーク」 はセールス・トークとしてはいいネーミングです。 しかし、 それは多重化した 「ロジスティック回帰」 をそう形容しただけなのです。 実際、ニューロン (神経細胞) が幾段にも平面的層をなして連なり、 層の間をシナプスがつなぐという単純な (しつらえた) モデルはおよそ医学的実体とは異なります。
ニューロンの集合体は、ひとかたまりの立体状をなし ており必ずしも層に還元できるような単純なものではありません。 ニューロンも発火するだけではなく抑制 (inhibition) の機能もあります。 さらには自律神経の介入もあります。 ですから 「ニューラル」 は実際とは何の関係もありません。 統計用語です。
また、 今は「人工知能」が「はやり」になっていますが、人間は 「知能」だけで行動しているわけではなく、本能という概念もあります。人間の判断や行動は[本能+知能]という複合で説明されます。 よい例として災害時の人間の行動は、 知能よりは集団的本能にしたがうと考えられますが、 人工知能にはそれが理解できません。
なので、ニューラルネットーワークの仕組みを大雑把でも理解していると、ちまたで繰り広げられている「AI」 や 「機械学習」「深層学習」に関する面白おかしい議論はの大半本質や真実に触れているものはあまりないということに気付くと思います。
まずはしっかりと中身の演算の理論を学ぶことが大切です。 そのために、ニューラルネットーワークやベイズ統計学を学ぶことは、 もっとも効率的で濃密な学び方なのです。そしてディープラーニングは実際に人間の脳を模しているものではありませんが、これまで人間が出すことの難しかった答えを簡単にだすことができているのはれっきとした事実であり、ここにさらに強化学習を加えることで、AIの知能は人間をはるかに超越する可能性があります。
現在、深層学習関連の研究は指数関数的に進んでおり、AIが人間を超えるシンギュラリティの到来もそう遠い未来ではないと言われています。AIだけでは計算するにとどまりますが、ここにインターネットとモノをつなぐIoTが加わることで社会はさらなる段階へ発展していくと思われます。
そして、ニューラルネットワークのプロセスをプログラミング言語で表現するのは超手間がかかりますが、pythonならTensorflowやkerasを使うことで簡単に実行することができるのでAIの実用化が進みニューラルネットワークやディープラーニングの重要性が高まる今Pythonの人気も高まりつつあります。
それに加えてPythonは他のプログラミング言語よりも比較的簡単にコードを書ける、エンジニアの平均年収が高いなどという利点もあるので、別にディープラーニングをしなくても初心者が最初に始めるプログラミング言語としてもオススメだと思います。
機械学習やディープラーニングが昔は独学で勉強するものでしたが、昨今は月々たった3000円でディープラーニングが勉強できる「オンラインPython学習サービス「PyQ™(パイキュー)」などもできており昔よりも学習のハードル・コストは下がりつつあります。
また他にも少し値段は高いですが、「人工知能特化型プログラミング学習サービス「Aidemy Premium Plan」だとレベルが高い学習内容なのでAIエンジニアとして実務レベルのスキルを身に着けられます。IT人材の給料が世界と比べて低い日本でもAIが分かるエンジニアには年収1000万を出すところもあるので、本気で勉強する気があるならば十分元はとれます。







コメント
[…] 関数そのものが理解できなかったのですが、わかりやすく説明されているサイトさんがあって、非常に助かりました。 【初心者向け】ニューラルネットワークを超分かりやすく解説する […]